Example DFA
Example DFA¶
The first pattern we will look at is a little complex. This will show some of the functionality we can build using simple DFA.
We want to look at a string made up of just a and b characters. We are looking for one that meets the following requirements.
Contains at least 1 b
Does not end in an odd number of a
Let’s imagine that we are reading a string. When we start, we have not seen any letters yet. Let’s make our first state q1. The state q1 basically means no requirements have been meet.
When a DFA has not read anything we say it has read the empty string. It is possible to accept the empty string. Maybe having no input is the correct answer to your problem.
We start at q1. What can happen? We could see an a character. We still don’t meet any of our requirements. Actually, we could see a million a characters in a row and never meet the first requirement. If we are in q1 and see an a, then we just stay in q1.
Transition 1: if q1 and a then q1
Our string might contain b. If we are in q1 and see we a b what does that mean? We absolutely meet requirement 1. We make up a second state q2. This state means “meets requirement 1 and 2.” Why does it meet requirement 2? If this is b is the last character we every see, then the string can’t end in a odd number of a. It is currently ended with a b.
Transition 2: if q1 and b then q2
We have introducted a second state. We now need to ask what happens in it. If we are in state q2 and see an a what does that mean? We still meet requirement 1, we have seen a b. We no longer meet requirement 2. The last character we saw was an a. Now, we have one a at the end. One is an odd number. We need a third state q3. The state q3 means “meets requirement 1 but not requirement 2”.
Transition 3: if q2 and a then q3
That is only one possibility in q2. What if we are in q2 and see b? Then both requirements are still met. We have more than one b. The current end of the string is currently a b. We can just stay in q2.
Transition 4: if q2 and b then q2
There is still one state with no transitions, state q3. What happens if state q3 sees an a. If this happens, we have 2 a at the end. This is an even number. All the requirements are met again.
Transition 5: if q3 and a then q2
Lastly, we could be in q3 and see a b. In this case, the last character read is a b. That means all requirements are met. We can transition back to q2.
Transition 6: if q3 and b then q2
If we keep following this pattern for every letter in the string, eventually we will get to the end. If we end in state q2 then all requirements were met.
The DFA is shown below.
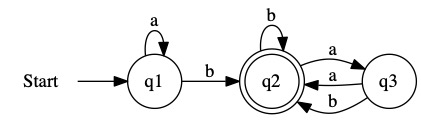
The full source code is given below.
#Define DFA Properties
symbols=(a,b)
states=(q1,q2,q3)
start=q1
accept=(q2)
#Define Transition Table
if q1 and a then q1
if q1 and b then q2
if q2 and a then q3
if q2 and b then q2
if q3 and a then q2
if q3 and b then q2
