Introduction to Graphs
Contents
Introduction to Graphs¶
Graphs provide an abstract model for representing relationship between things. This might sound really vague. It is! That is one of the beautiful things about graphs. They are a very abstract concept we can implement using data structures and algorithms. We can represent many different real world applications as graphs.
The basic components of a graph are nodes and edges.
Node: An object, normally with some properties related to it. Also called a Vertex in some contexts.
Edge: A relationship between two nodes. Sometimes it has properties associated with it as well.
There are two kinds of graphs. In an undirected graph, every edge connects in both ways. Think about Facebook. If you are friends with someone else, they are also friends with you. The friend connection on Facebook is always two-way. There are also directed graphs. In these graphs, an edge might only create a relationship in one direction. On Twitter, you might follow someone, but that does not mean they follow you back. The relationship only connects in one direction.
Graphs are very visual data structures. They are actually much easier to visualize than to program. We draw nodes as circles with their names written inside. A directed edge is a line with an arrow, the arrow shows the direction the relationship holds. If the edge has an properties, they are written on the line.
An undirected edge doesn’t have the little arrows.
It can be confusing to mix the two types of edges. In general, you should either have all undirected edges or all directed edges. If you want a directed edge to go both ways, you can always draw two lines. This makes it more clear to the reader.
A graph can also be weighted or unweighted. In an unweighted graph, all we care about is if the relationship exists. In a weighted graph there is some value related to the relationship. For example, if we make a graph of airports and connected them by plane flights, the flights have a cost. You cannot travel one one airport to another for free, you need to buy a ticket.
Graph Representations¶
There are two primary data structures used to represent graphs. Each has it’s own advantages and disadvantages. The adjacency matrix stores the graph into a matrix. This has a fast runtime but uses a lot of memory. The adjacency list stores the graph in an array of linked lists. This can use less memory, but requires a higher runtime.
We will look at the two structures conceptually before we look at their implementations.
We will start with a directed graph as our example.
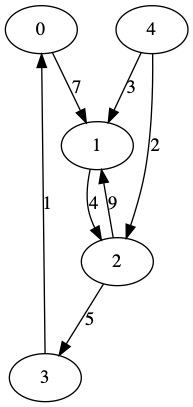
This graph has 5 nodes (0,1,2,3,4). For an adjacency matrix we make a \(n\) by \(n\) matrix. In this case, we need a \(5\) by \(5\) matrix. In each location, we place one of three values.
0 means travel over this edge has no cost
\(x \neq 0\) means the edge has a cost \(x\)
\(\infty\) means the edge does not exist
We will store the values in a matrix where the row is the from node and the column is the to node. Position M[a][b] stores the cost to travel from node a to node b.
| M[from][to] | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 7 | ∞ | ∞ | ∞ |
| 1 | ∞ | 0 | 4 | ∞ | ∞ |
| 2 | ∞ | 9 | 0 | 5 | ∞ |
| 3 | 1 | ∞ | ∞ | 0 | ∞ |
| 4 | ∞ | 3 | 2 | ∞ | 0 |
The diagonal of the matrix is all zeros. It is free to move from node 1 to node 1, actually you don’t move at all. The diagonal is telling us it is free to stay were you are. There is an edge of length 5 from node 2 to node 3, this is shown as M[2][3]=5. There is no edge connecting node 1 to node 0, this is why that position has an infinity.
If the graph has \(n\) nodes, the matrix always has \(n^2\) spaces. This means the memory usage of the matrix will always be \(O(n^2)\), even if barely any edges exist.
An adjacency list also has \(O(n^2)\) worst case memory usage, but it can take advantage of missing edges. We create an array of linked lists. We store only the edges that exist and their weights. Edges not stored in the data structure are assumed to not exist. The diagonal is assumed to be zero. This sames memory, but will cost us in implementation.
The same graph is represented as an adjacency list below.
| From | To List (node, weight) |
|---|---|
| 0 | (1,7) |
| 1 | (2,4) |
| 2 | (1,9), (3,5) |
| 3 | (0,1) |
| 4 | (1,3),(2,2) |
If every possible edge exists, there will still be \(n^2\) edges. In many situations, we work with what is called a sparse graph. This means that the majority of the edges are non-existent. In an adjacency matrix, we still need to store infinity in the matrix for all these non-existent edges. In an adjacency list, we can save space in these cases.
Graph Interface¶
We can write any graph algorithm using either of these methods. As we have already seen, each has its own strengths and weaknesses. We can create an interface that defines what a Graph is. We can then implement this with either method. This will allow us to switch out which graph Data Structure we use as needed.
The following are some example features we might want a graph to have. This abstraction is about how we want to imagine the graph works, not how it does work behind the scenes.
//Create An Empty Graph
Graph* emptyGraph(int nodes);
//Add an Edge to the Graph
void addEdge(Graph* G, int from, int to, int weight);
//What number represents Infinity in the graph?
int getInfinity();
//How many nodes are in the graph?
int numberNodes(Graph* G);
//What is the weight of edge (x,y)?
int weight(Graph* G, int x, int y);
//What nodes are Adjacent to node x?
nodeList* adjacentTo(Graph* G, int x);
//Clear Memory
void delete(Graph* G);
Example Main Program¶
We can write code that uses this interface. We don’t care which implementation is used. As long as the features work, this code will work.
int main(int argc, char** argv){
//Ask for the number of nodes
printf("How many nodes in the graph? \n");
int countNodes = readInt();
printf("Graph has %d nodes\n",countNodes);
//Make the Graph
Graph* G = emptyGraph(countNodes);
//Ask Number of Edges
printf("How Many Edges do you want to add?\n");
int numEdges = readInt();
//Ask for the edges
printf("Enter %d Edges as from to weight:\n",numEdges);
for(int i=0; i < numEdges; i++){
int from = readInt();
int to = readInt();
int weight = readInt();
addEdge(G,from,to,weight);
}
//Ok Lets test the graph
//Try printing out all the edges
for(int i=0; i < numberNodes(G); i++){
for(int j=0; j < numberNodes(G); j++){
if(weight(G,i,j)==getInfinity()){
printf("Edge from %d to %d has weight infinity\n",i,j);
}else{
printf("Edge from %d to %d has weight %d\n",i,j,weight(G,i,j));
}
}
}
//Check that the Adjacent List is correct
for(int i=0; i < numberNodes(G); i++){
nodeList* A = adjacentTo(G,i);
printf("Nodes Adjacent to %d [",i);
for(int j=0; j < A->count; j++){
printf("%d",A->nodes[j]);
if(j+1<A->count){
printf(", ");
}
}
printf("]\n");
free(A->nodes);
free(A);
}
//Free Memory
delete(G);
return 0;
}
If we want to make the following graph (remember arrays start at 0 instead of 1 in C). We can enter the right edges.
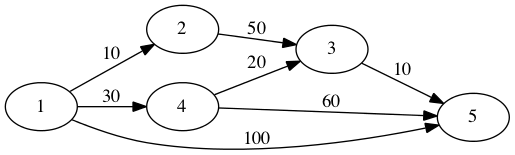
This is defined with the following inputs.
5
7
0 1 10
0 2 30
0 4 100
1 2 50
3 2 20
3 4 60
2 4 10
An example execution is shown below.
How many nodes in the graph?
5
Graph has 5 nodes
How Many Edges do you want to add?
7
Enter 7 Edges as from to weight:
0 1 10
0 2 30
0 4 100
1 2 50
3 2 20
3 4 60
2 4 10
Edge from 0 to 0 has weight 0
Edge from 0 to 1 has weight 10
Edge from 0 to 2 has weight 30
Edge from 0 to 3 has weight infinity
Edge from 0 to 4 has weight 100
Edge from 1 to 0 has weight infinity
Edge from 1 to 1 has weight 0
Edge from 1 to 2 has weight 50
Edge from 1 to 3 has weight infinity
Edge from 1 to 4 has weight infinity
Edge from 2 to 0 has weight infinity
Edge from 2 to 1 has weight infinity
Edge from 2 to 2 has weight 0
Edge from 2 to 3 has weight infinity
Edge from 2 to 4 has weight 10
Edge from 3 to 0 has weight infinity
Edge from 3 to 1 has weight infinity
Edge from 3 to 2 has weight 20
Edge from 3 to 3 has weight 0
Edge from 3 to 4 has weight 60
Edge from 4 to 0 has weight infinity
Edge from 4 to 1 has weight infinity
Edge from 4 to 2 has weight infinity
Edge from 4 to 3 has weight infinity
Edge from 4 to 4 has weight 0
Nodes Adjacent to 0 [1, 2, 4]
Nodes Adjacent to 1 [2]
Nodes Adjacent to 2 [4]
Nodes Adjacent to 3 [2, 4]
Nodes Adjacent to 4 []
Adjacency Matrix Implementation¶
An Adjacency Matrix is just an array of arrays. We also need to track the number of nodes so we know how many spaces are in our array.
typedef struct AdjMatrix Graph;
struct AdjMatrix{
int** M;//Matrix to store weights
int nodes;//The number of nodes
};
To create an empty graph, we first allocate a pointer of rows. For each row, we make an array for the columns. We will all the positions in with \(\infty\). The diagonal of the matrix is filled with zeros.
Graph* emptyGraph(int nodes){
//Make an array of pointers
int** pointers = malloc(nodes*sizeof(int*));
//For each position put an array
for(int i=0; i < nodes; i++){
pointers[i]=malloc(nodes*sizeof(int));
}
//We now have enough space
//Fill with infinity in all locations
for(int i=0; i < nodes; i++){
for(int j=0; j < nodes; j++){
pointers[i][j]=getInfinity();
}
}
//Put zero on diagonal
for(int i=0; i < nodes; i++){
pointers[i][i]=0;
}
//Update Data Stucture
Graph* G = malloc(sizeof(Graph));
G->M = pointers;
G->nodes = nodes;
return G;
}
We can very easily add an edge. We just update the correct position in the matrix.
void addEdge(Graph* G, int from, int to, int weight){
G->M[from][to]=weight;
}
There is no \(\infty\) in your computer’s hardware for integers. We can make up a value that works. To write general code, we provide a function to check what number means infinity. We use the largest integer the hardware can store. Note: What happens if you add 1 to INT_MAX?
int getInfinity(){
return INT_MAX;//From limits.h
}
The number of nodes in the graph is trivial to find.
int numberNodes(Graph* G){
return G->nodes;
}
The best thing about the Adjacency Matrix is how easy it is to find the weight of an edge.
int weight(Graph* G, int x, int y){
return G->M[x][y];
}
To delete the entire thing, we need to delete each row first.
void delete(Graph* G){
for(int i=0; i < G->nodes; i++){
free(G->M[i]);
}
free(G->M);
free(G);
}
To return the Adjacent Nodes, we need some data structure to hold the results. This will allow us to return a list of nodes without the programmer using our graph knowing how we built it.
//An array of nodes paired with
//its size
typedef struct nodeList nodeList;
struct nodeList{
int* nodes;
int count;
};
We search the graph for any non-infinity edges. If there is an edge to another node, then it is adjacent.
nodeList* adjacentTo(Graph* G, int x){
//Create a new array
int* adjacent = malloc(G->nodes*sizeof(int));
//Only Copy in non-infinity values
//Also skip self
int pos=0;
for(int i=0; i < G->nodes; i++){
if(weight(G,x,i)!=getInfinity() && i!=x){
adjacent[pos]=i;
pos++;
}
}
//Made a nodeList
nodeList* nl = malloc(sizeof(nodeList));
nl->nodes = adjacent;
nl->count = pos;
return nl;
}
Adjacency List Implementation¶
The Adjacency List is a little more complicated to build. We need a simple linked list structure to start with. This is a specialized implementation just for our needs.
//We need a limited linked list structure
typedef struct LinkedList LinkedList;
typedef struct EdgeNode EdgeNode;
struct LinkedList{
EdgeNode* head;
};
struct EdgeNode{
int from;
int to;
int weight;
EdgeNode* next;
};
It has two features of it’s own. We can make a new linked list using the below function.
//Linked List Helpers
LinkedList* makeLL(){
LinkedList * L = malloc(sizeof(LinkedList));
L->head = NULL;
return L;
}
We can add or update an edge. If the to and from values are already in the graph, we update the value. If not, we add a new node to the front of the linked list. You will remember from Stacks and Queues that adding to the front and back of a linked list is the easiest.
//Put this node in front of the list
void addTo(LinkedList* L,int from, int to, int weight){
//See if already here overwrite
EdgeNode* n = L->head;
while(n!=NULL){
if(n->to ==to && n->from==from){
n->weight=weight;
return;
}
n=n->next;
}
//Insert
EdgeNode* N = malloc(sizeof(EdgeNode));
N->from = from;
N->to = to;
N->weight = weight;
N->next = L->head;
L->head=N;
}
Now, we can make our graph. It has an array of linked lists.
//Graph Structure
typedef struct AdjList Graph;
struct AdjList{
//Array of pointers to edge nodes
LinkedList** edgeInfo;
int nodes;
};
We can still make an empty graph. It is an array of empty linked lists.
Graph* emptyGraph(int nodes){
//Make Structure
Graph* G = malloc(sizeof(Graph));
//Set Node Count
G->nodes = nodes;
//Create Array
G->edgeInfo = malloc(nodes* sizeof(LinkedList*));
//Set all positions to null
for(int i=0; i < nodes; i++){
G->edgeInfo[i] = makeLL();
}
return G;
}
We can just use the Linked List’s features to add new edges.
void addEdge(Graph* G, int from, int to, int weight){
LinkedList* L = G->edgeInfo[from];
addTo(L,from,to,weight);
}
We still need to know what represents infinity in the graph.
int getInfinity(){
return INT_MAX;
}
We can easily find out the number of nodes.
int numberNodes(Graph* G){
return G->nodes;
}
Finding the weight of an edges has become more difficult. We know which linked list it is in, but not where. We need to search the linked list to find the weight.
int weight(Graph* G, int x, int y){
//We can always reach ourselves
if(x==y){return 0;}
//We need to find it!
LinkedList* L = G->edgeInfo[x];
//Loop over the list
EdgeNode* node = L->head;
while(node!=NULL){
if(node->to == y){
return node->weight;
}
node = node->next;
}
//Never Found!
return getInfinity();
}
The function to find Adjacent Edges nodeList* adjacentTo(Graph* G, int x) is unchanged! It only used functions we already implemented. It did is the same for both data structures.
To delete the graph from memory, we need to delete every node and every linked list.
void delete(Graph* G){
//Loop over every linked list
for(int i=0; i < G->nodes; i++){
//Loop over every node
EdgeNode* n = G->edgeInfo[i]->head;
while(n!=NULL){
EdgeNode* temp = n;
n = n->next;
free(temp);
}
free(G->edgeInfo[i]);
}
//Free the Graph
free(G);
}
Summary¶
The Adjacency Matrix uses \(O(n^2)\) memory for \(n\) nodes. It needs to make space for every edge that count possibly exist. This makes edge lookups and changes \(O(1)\). We trade memory for speed.
On the other hand, the Adjacency List only needs to use memory for edges that exist. It could use as much as \(O(n^2)\) but it can use a minimum of \(O(n)\). When the graph is sparse, it contains few edges, we will have high memory savings. The Adjacency List needs more complex algorithms to access and update edge weights in exchange for saving memory.
Each of these data structures has advantages and disadvantages. You need to think about your problem and which will work best with the graphs you are planning to work with.
