Stack
Contents
Stack¶
A stack is a Data Structure that can grow and shrink as needed. It is a type of Linked List.
Stack Abstract Data Type¶
Imagine you have 10 plates in a stack. It is easy to remove the top plate. It is hard to remove the middle plate. It is very hard to remove the bottom plate. To get to a plate deep in the pile, we need to move every higher plate first. On the other hand, adding and removing from the top of the stack of plates in very easy.
Our stack of plates has the following functionality:
Create a new stack of plates
Check there are no plates left
Add a plate to the top
Remove the top plate
Look at the top plate
This can form the foundation for an Abstract Data Type. The Abstract Data Type needs the following functionality.
Create a new stack
Check if the stack is empty
Push a new value onto the top of the stack
Pop the top value off the top of the stack
Look at the top value on the stack
This gives us a conceptual model for the stack. We can build it using a Linked List of Nodes.
Nodes and Pointers¶
An array is just a sequence of values in memory. We can take advantage of the fact that they are all next to each other. We can predict the memory address of a specific value. When we say A[3], we are saying move 3 spaces after the first memory address in the array A.
We can use memory addresses to build efficient algorithms. What if we don’t know how many values we need to store? Resizing arrays is not easy. If there is no available memory next to the current array, we need to move all our values.
Linked Lists are way to store data that can be dynamically resized. Direct references to memory address are key to this ability. When we store a memory address it is called a pointer.
A variable is the actual value stored in memory. A pointer is the memory location of the value.
A Linked List is a kind of Data Structure. It can be used to implement many Abstract Data Types.
An Abstract Data Type is a theoretical model that describes the behavior data. The abstract part tells us we are not worrying about the implementation, only the ideas.
A Data Structure is the realization of an Abstract Data Type. The Data Structure is what we actually implement.
We can talk about an Array as an Abstract Data Type. We might say that we need to be able to access and change values in the array. This is a universal concept about arrays. We can also talk about a C++ array. This would be a Data Structure. How does C++ actually implement and use arrays? It might be different then Java or Python.
There can be many implementations of a single Abstract Data Type. Each implementation is a unique Data Structure.
Nodes¶
The Abstract Data Type for the Node is a kind of record. We need to know two things.
What is the current value?
What is the next value in the data set?
We also what the following functionality. This is the feature an array does not have.
Add new elements to beginning of data set
Add new elements to middle of data set
Add new elements to end of data set
That is what we want to happen. The Data Structure is how we will implement it. For the Node Data Structure we need two values.
value - The value stored in this node
next - A pointer to the location in memory the next value is stored.
The next pointer is key to our functionality. We can change this memory location to add new elements and resize a sequence of values dynamically.
We also need a special value to me no more elements. This is traditionally called the null, none, or nil. It depends what language you are using. There is always some special name for the empty memory address. This is a way to make a pointer that points to nowhere. We will use NULL in the examples.
The Node data structure is fairly simple. It is just two values placed next to each other in memory.
//The Node Data Structure
typedef struct node Node;
struct node {
int value; //The Value Stored at this node
Node* next; //Pointer to the next value
};
Stack Data Structure¶
The Node isn’t very interesting on its own. It is useful at a low level, but we can build more interesting things using it. A Linked List is a series of Nodes connected together. We can build many Data Structures based on this concept. The first one we will look at is the Stack.
To implement the stack we need to store values somewhere. We only need to know where the top of the stack is. We traditionally call this the head of the stack.
The stack needs a pointer to the top value. We call this pointer the head of the stack. This head pointer will point to a Node. We can dig deeper into the stack by following next pointers.
The stack’s data is fairly simple. It is the algorithms we write to work with it that make it interesting.
//A Stack
typedef struct stack Stack;
struct stack {
Node* head; //The first element on the stack
};
The Data Structure also has a collection of functions that work on it. We call functions related to a specific structure operations. In Object Oriented Design, the structure and functions are collected into one object called a class. This is not required, it is just a useful way to organize the code.
Stack Operations¶
The stack needs to be able to do everything our Abstract Data Type described.
newStack()- Create a new empty stackisEmpty(S)- Determine if stackSis empty or notpush(v, S)- Add valuevto the top of stackStop(S)- Look at the value on top of stackSpop(S)- Remove the top value of stackS
To create a new stack we need to allocate a pointer to the structure. We just point the head to nil because there are no elements.
//Create a new Stack
Stack* newStack(){
Stack* S = malloc(sizeof(Stack));
S->head = NULL;
return S;
}
To determine if the stack is empty, we just need to check if head points to the NULL element or a valid location in memory.
//isEmpty: Check if stack is empty
bool isEmpty(Stack* S){
if(S->head == NULL){
return true;
}
return false;
}
To check the top element in the stack, we just need to look at the value of the head node. If the stack is empty we return -1 here. This may be a situation where an error would be needed in a practical implementation.
//Top: Find out the top value on the stack
//Return -1 if no value
int top(Stack* S){
//Check for Empty
if(S->head == NULL){
return -1;
}
return S->head->value;
}
To push a new value onto the stack, we need a few steps. First, we need to allocate memory for the new value. Once we have the memory allocated, we set the value. Finally, we need to connect up the memory locations. We point the new node’s next value to the head. Then we make the new value the head. This inserts the new node at the front of the list.
//Push: add a Value onto the stack
//Input is a POINTER to the stack
void push(int value, Stack* S){
//Allocate a code and get pointer to it
Node* newNode = malloc(sizeof(Node));
//Add values to new Node
newNode->value = value;
newNode->next = S->head;
//Add to Front of List
S->head = newNode;
}
To pop an element off the stack, we just need to move the head value forward one pointer.
//Pop: Remove top value
void pop(Stack* S){
if(S->head == NULL){
return;
}
Node* old = S->head;
S->head = S->head->next;
free(old);
}
There may be situations where we need to erase the stack. We can make use of pop to do this. It will need to pop all available values.
void erase(Stack *S) {
while (!isEmpty(S)) {
pop(S);
}
free(S);
}
Stack Runtimes¶
All stack operations are all constant time. This means if we solve a problem with a stack we don’t have to worry about the data structure slowing down out program. Each operation will run in constant time. The only operation that might not is erase, but that is only if the stack contains elements when it is called. If they are already popped, it will be \(O(1)\).
Method |
Runtime |
|---|---|
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(n)\) |
The stack is a low level data structure. It is frequently included in programming language libraries. It is also frequently used as part of more complicated algorithms. This makes it constant runtime very important. It won’t negatively impact the algorithms it is used with.
Postfix Calculator¶
Postfix notation is a method of writing mathematical operations where the operators come after the input. Instead of \(9+8\) we write \(9\) \(8\) \(+\). This notation never needs parenthesis, which can make it easier to handle order of operations. It is popular in financial calculators. It is also known as rpn or Reverse Polish Notation [Wikipedia contributors, 2020]. The polish part is a reference to the nationality of the notation’s inventor. It is not a insult like many people think.
Hewlett Packard has historically produced may rpn calculators [David G. Hicks, 2020]. The current HP-12 model is a traditional rpn calculator [HP Development Company, L.P, 2020].
Postfix notation is important two computer science for two reasons. First, order of operations is easy to manage. Secondly, it can be implemented using only a stack.
Postfix Evaluation¶
To evaluate an expression written in rnp, the algorithm is fairly simple.
While values to read
If a number then push onto the stack
If an operator
Pop the stack twice
Compute value
Push result onto stack
Result is final value on the stack
We can look at this algorithm using an example. We want to evaluate 3 4 * 7 +.
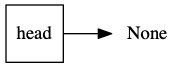
We start with the empty stack.
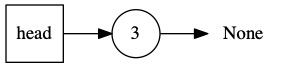
The first thing we see is the number three. We push three onto the stack.
The next value in the input 3 4 * 7 + is the number four. We again push onto the stack.

The next value is an operator. It is multiplication. We pop the top two values from the stack. Then we compute the result \(3*4=12\). We push the result back onto the stack.
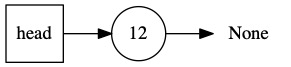
We still have more input to read from 3 4 * 7 +. The next value is the number seven. It is pushed onto the stack.

The last value in the input is another operator. It is the plus sign. We again pop the top two values and compute the result. We push \(12 + 7=19\) onto the stack.
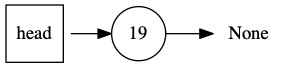
There are no values left to read in the input. The value on the top of the stack is the result of the current computations.
Postfix Implementation¶
We can use our stack to implement this concept. For the sake of simplicity, we will only deal with 1 digit letters. This is purely to make the code easier to read. The calculator would work exactly the same for multi-digit numbers. It would just be more code to parse out each digit.
Given a string of characters as input, we can use the stack to implement a postfix calculator
int compute(char* input){
//Create a New Stack
Stack* myStack = newStack();
//Split the string up on spaces
char** tokens = splitOnSpaces(input);
for(int i = 0; tokens[i]!=NULL; i++){
printf("TOKEN: %s\n",tokens[i]);
if(isNumber(tokens[i])){
int value = stringToInt(tokens[i]);
push(value, myStack);
}
if(isOperator(tokens[i])){
int b = top(myStack);
pop(myStack);
int a = top(myStack);
pop(myStack);
char operator = tokens[i][0];
int result = 0;
if(operator == '+'){
result = a + b;
}else if( operator == '-'){
result = a - b;
}else if(operator == '*'){
result = a * b;
}
push(result, myStack);
}
}
if(isEmpty(myStack)){
return 0; //Invalid Expression
} else {
int res = top(myStack);
pop(myStack);
return res; //Result of Last Computation
}
return 0;
}
This calculator looks at every value in the string exactly one time. It uses stack operations, which we already know are constant time. This means the runtime of the algorithm will be \(O(n)\) where \(n\) is the number of characters that need to be read. As a simple example, we can compute \((25*27)+12 - 125 = 312\).
int main(int argc, char** argv){
int x = compute("25 17 * 12 + 125 -");
printf("Result: %d\n",x);
return 0;
}
