.md .pdf

Contents

Search Methods

Searching is one of the most common problems in computer science. We have a large set of data and we need to find something in it.

Linear Search

The most straightforward solution to searching a list is a linear search. We start at the first element and check each one. If it is the target, we found what we are looking for. This is called a Linear Search.

We have an array of items we want to search. We know how many items there are in the array. We also know the item we are looking for. The function will return true if the item is found and false otherwise.

The basic approach to the algorithm is to just start at the beginning. Look at every item. If it is the target we return true. If not, we keep going. Eventually, we will either find what we are looking for or run out of values to check.

We will look at the algorithm using pseudocode first.

Function linearSearch(int needle, array haystack, int size)
    Let i = 0
    While i < size do 
        If needle is at index i of haystack then 
            Return True
        End If
        i = i + 1
    End While
    Return False
End Function

This function is reasonably easy to trace. Let us look at an example.

• Array haystack contains [2,4,6,8]

• The number of elements size is 4

• The target value needle is 7

The code does the following:

1. Compares 7 to 2 and finds they are different

2. Compares 7 to 4 and finds they are different

3. Compares 7 to 6 and finds they are different

4. Compares 7 to 8 and finds they are different

5. Determines there are no more numbers to compare to.

6. Returns False.

When we reach step 5, we know we can return False.

What is instead we changed our target to 6.

1. Compares 6 to 2 and finds they are different

2. Compares 6 to 4 and finds they are different

3. Compares 6 to 6 and finds they are the same.

4. Returns True

When we find the target, we return True. The target was in this list, so we found it and returned the correct answer.

Implementation

We can implement the pseudocode in C.

bool linear(int n, int* h, int size){
    for(int i=0; i < size; i++){
        if(n==h[i])
            return true;
    }
    return false;
}

We used a for loop here to simply the code. It does change anything significantly about the while loop in pseudocode. It just makes it easier to read. The for loop will release the variable i when it is done, but the code returns immediately anyway. This is not a notable difference for this example.

The if statement does not have brackets because it is only one line. If no brackets are given one line is matched to the if. This also makes the code a little prettier.

We can repeat the two tests from above in C.

int main(int argc, char** argv){
    //Simple Example
    int haystack[4] = {2,4,6,8};
    int size = 4;
    //Test 1:
    bool res1 = linear(7,haystack,size);
    bool res2 = linear(6,haystack,size);
    printf("Result of Test 1: %d\n",res1);
    printf("Result of Test 2: %d\n",res2);
    return 0;
}

The output of the code is shown below. Not that C just uses \(0\) and \(1\) for true and false. These are defined in a library. To get the bool data type you need to include “stdbool.h”.

Result of Test 1: 0
Result of Test 2: 1

We will look at the memory usage of this function first. An int needs 4 bytes. An int* needs 8 bytes. A bool needs 1 byte.

We take two int variables and one int* as inputs to the function. We return a single bool. No dynamic memory is allocated on the heap during this functions execution. We have one int using locally.

• Inputs: 16 bytes

• Returns: 1 byte

• Local Variables: 4 bytes

• Heap Memory: 0 bytes

The amount of memory this function uses is constant. It never changes no matter how big the array we are searching is.

When look at the runtime, things get trickier. We can assume the array has some size. What we don’t know is when the loop will find the target.

Once case is when the size is 0. In this situation, we would assign i to zero. Then the condition would check i < size which would be false. The function would immediately return. In this situation, we only executed a few commands.

Operation	Count
=	1
<	1
for	1
return	1

This is clearly a constant number of operations. We have \(T(n)=4\), but it is a special case, not a general answer.

What if we have a long array with size items in it. The target is never found in the list. The for loop needs to run all the way up to size. The loop would do one assignment at the start. It would count all the way up to size. The means the i++ needs to execute size times. The comparison i < size needs to run size+1 times. It is true size times and false once. The for checks the result of this comparison every time. The if statement checks if(n==h[i]) for every iteration of the loop. There is one return at the end. In this case, the number of operations is shown below.

Operation	Count
=	1
for	size+1
<	size+1
++	size
==	size
if	size
[]	size
return	1

In this case, we have \(T(\text{size}) = 6 * \text{size}+4\).

We could also find the answer somewhere in the middle. We could have the if statement return true at some point. Let’s imagine it found the target at the halfway point. Then we would have \(T(\text{size}) = 6 * \frac{\text{size}}{2}+4\).

It looks like there are a lot of possible run times for this search. That is true, but we can still classify the algorithm. We want to approximate the number of operations. To do so, we use a notation called Big Oh. In Big Oh notation we want to give an upper bound on the number of operations. This is an approximation of the worst case. It tells us about the maximum time the code could take to run.

We want to say that the number of operations this algorithm needs is always less than some constant \(c\) times the size. We won’t define the constant. We are just trying to say the following.

\( \begin{align} T(n) & < c * \text{size} \\ 6 * \text{size}+4 & < c * \text{size} \end{align} \)

In Big Oh notation, we would say \(T(\text{size}) = O(\text{size})\). This is saying that the function is linear. It is a function \(a*\text{size}+b\) but we are ignoring what exactly \(a\) and \(b\) are. If it was a quadratic function \(a*\text{size}^2+b*\text{size}+c\) we would say \(T(\text{size})=O(\text{size}^2)\). If it was a constant function like \(T(n)=7\) we would say \(T(n)=O(1)\). We don’t care what the exact constants are in the formula. In this case, we cannot actually be sure ourselves. We are trying to classify the runtime. In our case, the linear search’s number of operations is clearly a line going up as size increases. That is the most important concept. We could say the memory \(M(\text{size})=O(1)\) because the memory usage is always constant.

• Memory Usage of Linear Search: \(O(1)\)

• Runtime of Linear Search: \(O(n)\)

Testing

It doesn’t help much if we write code that doesn’t work. Linear Search works conceptually. We need to make it work in practice. This means we need to test our code.

We need a test plan. We don’t know if the search works. We need to somehow generate tests where we can predict the outcome. The if our search is correct it will return our predicated output. If not, we will detect an error.

Here is our proposal. We will generate arrays with even numbers in them. Then we will search them for even and odd numbers. We can predict the answer to the search finding the remainder of division.

Our basic plan will be as follows:

1. Generate an array of even numbers from 0 to 2n-2

2. Search from -1 to 2n+1

3. Compare result of linear search and our prediction

To generate random arrays, we need to use the random number generator. The C random number generator must be seeded. This means we give it a number to compute the starting point with. If we give the random number generator the same seed it will generate the same numbers. This is nice for testing. When we want to use more random numbers, we can seed with the time. We only seed a random number generator once per in a program. If we seeded twice, it would reset the generator and not get us a good distribution of numbers.

The code in main will run tests for many sizes.

//Random Testing
//Seed the Number Generator
srand(time(NULL));
//run test for multiple sizes
for(int i=0; i < 100; i++){
    int* temp = randArray(i);
    printf("Testing Arrays of Size %d\n",i);
    bool result = testArray(temp,i);
    if(result){printf("All Tests Passed\n");}
    free(temp);
}

We need to generate our array in a predictable way. First, we allocate an array with n spaces for integers. We will fill this array with numbers in order. We run i from 0 to n. We put the value \(2n\) in the array. This will get us the range \(0,2,4,\cdots,2(n-1)\). Having the values in order is probably not the best test. In the real world, they could be in any order. After filling the array, we shuffle it. We select a random number as an index and swap two values. This will shuffle up the values.

//Implemenation of Random Array Generation
int* randArray(int n){
    //Make Array
    int* A = malloc(n*sizeof(int));
    int temp;//For swapping later
    int target;//Where to swap
    int i;//For counters
    //Insert Even Numbers
    for(i=0; i < n; i++){
        A[i] = i*2;
    }
    //Shuffle
    //Swap every value with a random position
    for(i=0; i < n; i++){
        target = rand()%n;
        //Swap values at i and target
        temp = A[i];
        A[i] = A[target]; 
        A[target] = temp;
    }
    //Return the array we made
    return A;
}

Now, we want to test the array. We loop over all numbers in the range from \(-`\) to \(2n+1\). We can predict if the value is in the array or not. If the result of linear search is not the same as our expected value, we print an error. If all tests pass we return true.

//Test on Array
//Since we made the array we know what it should look like
bool testArray(int* A, int n){
    int start=-1;//-1 is never in the array
    int stop = 2*n+1;//Also never in the array
    for(int i=start; i <=stop; i++){
        //What does linear search say?
        bool lsearch = linear(i,A,n);
        //What do we expect?
        //If it is even in range we expect true
        bool expect = i>=0 && i < 2*n && i%2==0;
        //Error
        if(lsearch != expect){
            printf("******START ERROR********\n");
            printf("Search for %d\n",i);
            printf("Answer: %d\n",lsearch);
            printf("Expected Answer: %d\n",expect);
            printf("Array Used:\n");
            printArray(A,n);
            printf("******END ERROR********\n");
            return false;
        }
    }
    return true;
}

It is useful to make a helper function to make printing the array easier.

void printArray(int* p, int n){
    printf("[");
    for(int i=0; i < n; i++){
        printf("%d",p[i]);
        if(i+1 < n){
            printf(", ");
        }
    }
    printf("]\n");
}

If our linear search has a problem, we will get an error message. Then we can fix the issues.

Testing Arrays of Size 54
******START ERROR********
Search for 10
Answer: 0
Expected Answer: 1
Array Used:
[66, 38, 98, 96, 20, 46, 36, 14, 74, 76, 28, 22, 6, 16, 40, 2, 8, 44, 78, 48, 34, 52, 42, 86, 50, 92, 64, 54, 88, 56, 60, 24, 72, 94, 70, 26, 104, 84, 4, 106, 18, 90, 0, 68, 102, 82, 30, 12, 62, 32, 100, 58, 80, 10]
******END ERROR********

If our code works, we get a confirmation.

Testing Arrays of Size 0
All Tests Passed
Testing Arrays of Size 1
All Tests Passed
Testing Arrays of Size 2
All Tests Passed
Testing Arrays of Size 3
All Tests Passed
Testing Arrays of Size 4
All Tests Passed
Testing Arrays of Size 5
All Tests Passed
Testing Arrays of Size 6
All Tests Passed
Testing Arrays of Size 7
All Tests Passed
...

This test is not a guarantee that our code works. We know it works for this situation. If we combine that fact that these tests work with our early understanding of why the algorithm is correct that should make us more confident. We could add further tests to build more confidence.

Experimental Analysis

At this point, we are pretty sure the code works. Next, we want to know if it is actually as fast as we thought. We can time code. All we need to do is:

1. Get the time before code runs

2. Run some code

3. Get the time after code runs

4. Subtract the before and after times

In C, we can ask the system how many times the processor clock ticked between code execution. This is not the literal time that passed because it only counts time our program was using the processor. It very useful for this kind of timing question. This is part of the time.h library.

int before = clock();
bool res3 = linear(6,haystack,size);
int after = clock();
printf("Code Took: %d Clock Ticks\n", after-before);
printf("The Clock Ticks %d times per second.\n",CLOCKS_PER_SEC);

The problem with this is, every test might be different. Here are four test runs.

Code Took: 5 Clock Ticks
The Clock Ticks 1000000 times per second.

Code Took: 7 Clock Ticks
The Clock Ticks 1000000 times per second.

Code Took: 9 Clock Ticks
The Clock Ticks 1000000 times per second.

Code Took: 5 Clock Ticks
The Clock Ticks 1000000 times per second.

To get an accurate measure, we are going to need to average a number of tests. If we run 100 tests and average the results, that will tell us more than any one test will. We can reuse our random array generator from the testing section.

//Run t tests on size n and average
float averageTime(int n, int t){
    int total = 0;
    int* X = randArray(n);
    for(int i=0; i < t; i++){
        //Pick a random number 0 to 2n (exclusive of 2n)
        int target = rand()%(2*n);
        int before = clock();
        bool t = linear(target,X,n);
        int after = clock();
        total = total + (after-before);
    }
    free(X);
    return (float)(total)/(float)(t);
}

Now we should get a slighlty more useful result.

float testTime = averageTime(10,1000);
printf("Code Took: %0.2f Clock Ticks\n", testTime);
printf("The Clock Ticks %d times per second.\n",CLOCKS_PER_SEC);

For example,

Code Took: 0.47 Clock Ticks
The Clock Ticks 1000000 times per second.

To really get a feel for what it happening we run many tests at many different sizes.

void runTimings(){
    printf("The Clock Ticks %d times per second.\n",CLOCKS_PER_SEC);
    printf("| %7s | %8s |\n","Size","Clocks");
    printf("| ------- | -------- |\n");
    int size = 1;
    for(int i=0; i < 20; i++){
        //Compute Timings
        float testTime = averageTime(size,1000);
        printf("| %7d | %8.2f |\n", size,testTime);
        size = size * 2;
    }
}

The output we get is shown below.

The Clock Ticks 1000000 times per second.
|    Size |   Clocks |
| ------- | -------- |
|       1 |     0.51 |
|       2 |     0.44 |
|       4 |     0.46 |
|       8 |     0.69 |
|      16 |     0.63 |
|      32 |     0.65 |
|      64 |     0.67 |
|     128 |     0.95 |
|     256 |     1.46 |
|     512 |     2.73 |
|    1024 |     4.57 |
|    2048 |     8.29 |
|    4096 |    13.47 |
|    8192 |    21.47 |
|   16384 |    31.37 |
|   32768 |    51.91 |
|   65536 |   104.38 |
|  131072 |   210.70 |
|  262144 |   430.07 |
|  524288 |   845.18 |

As a table it looks like the following.

Size	Clocks
1	0.51
2	0.44
4	0.46
8	0.69
16	0.63
32	0.65
64	0.67
128	0.95
256	1.46
512	2.73
1024	4.57
2048	8.29
4096	13.47
8192	21.47
16384	31.37
32768	51.91
65536	104.38
131072	210.70
262144	430.07
524288	845.18

To visualize this data, we can put it in a chart. If our prediction is correct, this plot should look like a line.

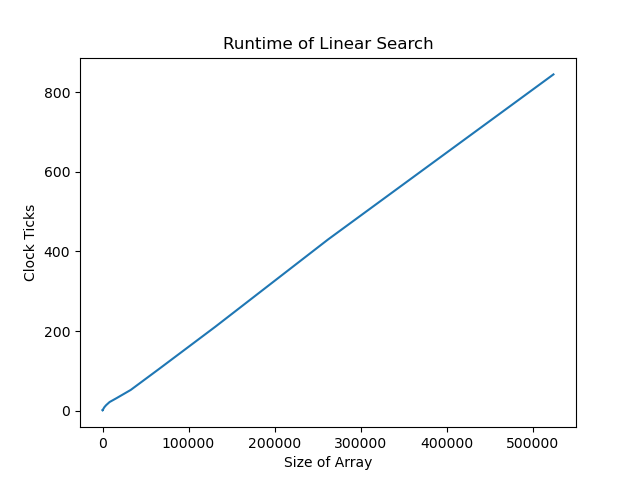
Just like with our tests, the experimental data lines up with our prediction. It is a linear time algorithm.

Full C Code

Here is the full C code for the examples above.

/**
  @file
  @author Mark Boady <mwb33@drexel.edu>
  @date January 13, 2022
  @section DESCRIPTION
 
  Analysis and Coding of Linear Search
 
 */

#include "stdio.h"
#include "stdlib.h"
#include "stdbool.h"
#include "time.h"
/**
 Linear Search of an Array of Numbers
 @param n is the target to search for
 @param h is a pointer to the array to search
 @param size is the number of elements in the array
 @return true if n is in h and false otherwise
 */
bool linear(int n, int* h, int size);
/**
 Generate a Random Array with n even numbers (Starting with 0)
 @param n is the size of the array you want
 @return Pointer to array created
 */
int* randArray(int n);

/**
 Print Array for Testing
 @param p is a pointer to an array
 @param n is the number of elements to print
 */
void printArray(int* p, int n);
/**
 Test Search Array A of size n for values -1 to 2*n+1
 We know that even number between 0 and 2n-2 should be found
 and no other numbers should be.
 @param A is the array to search
 @param n is the size of the array
 @return true if all tests pass and false on any failure
 */
bool testArray(int* A, int n);

/**
 Run multiple tests and return average time
 @param n is the array size to test
 @param t is the number of tests
 @return average clock ticks over all runs
 */
float averageTime(int n, int t);

/**
 Run many timing experiments and print a chart
 */
void runTimings();

int main(int argc, char** argv){
	//Simple Example
	int haystack[4] = {2,4,6,8};
	int size = 4;
	//Test 1:
	bool res1 = linear(7,haystack,size);
	bool res2 = linear(6,haystack,size);
	printf("Result of Test 1: %d\n",res1);
	printf("Result of Test 2: %d\n",res2);
	//Sizes
	printf("int: %lu\n",sizeof(int));
	printf("int*: %lu\n",sizeof(int*));
	printf("bool: %lu\n",sizeof(bool));
	//Random Testing
	//Seed the Number Generator
	srand(time(NULL));
	//run test for multiple sizes
	for(int i=0; i < 100; i++){
		int* temp = randArray(i);
		printf("Testing Arrays of Size %d\n",i);
		bool result = testArray(temp,i);
		if(result){printf("All Tests Passed\n");}
		free(temp);
	}
	//Compute Timings
	float testTime = averageTime(10,1000);
	printf("Code Took: %0.2f Clock Ticks\n", testTime);
	printf("The Clock Ticks %d times per second.\n",CLOCKS_PER_SEC);
	//Real Timings
	runTimings();
	return 0;
}

//Run Many Experiments
void runTimings(){
	printf("The Clock Ticks %d times per second.\n",CLOCKS_PER_SEC);
	printf("| %7s | %8s |\n","Size","Clocks");
	printf("| ------- | -------- |\n");
	int size = 1;
	for(int i=0; i < 20; i++){
		//Compute Timings
		float testTime = averageTime(size,1000);
		printf("| %7d | %8.2f |\n", size,testTime);
		size = size * 2;
	}
}

//Implementation of Linear Search
bool linear(int n, int* h, int size){
	for(int i=0; i < size; i++){
		if(n==h[i])
			return true;
	}
	return false;
}

void printArray(int* p, int n){
	printf("[");
	for(int i=0; i < n; i++){
		printf("%d",p[i]);
		if(i+1 < n){
			printf(", ");
		}
	}
	printf("]\n");
}

//Implemenation of Random Array Generation
int* randArray(int n){
	//Make Array
	int* A = malloc(n*sizeof(int));
	int temp;//For swapping later
	int target;//Where to swap
	int i;//For counters
	//Insert Even Numbers
	for(i=0; i < n; i++){
		A[i] = i*2;
	}
	//Shuffle
	//Swap every value with a random position
	for(i=0; i < n; i++){
		target = rand()%n;
		//Swap values at i and target
		temp = A[i];
		A[i] = A[target];
		A[target] = temp;
	}
	//Return the array we made
	return A;
}

//Test on Array
//Since we made the array we know what it should look like
bool testArray(int* A, int n){
	int start=-1;//-1 is never in the array
	int stop = 2*n+1;//Also never in the array
	for(int i=start; i <=stop; i++){
		//What does linear search say?
		bool lsearch = linear(i,A,n);
		//What do we expect?
		//If it is even in range we expect true
		bool expect = i>=0 && i < 2*n && i%2==0;
		//Error
		if(lsearch != expect){
			printf("******START ERROR********\n");
			printf("Search for %d\n",i);
			printf("Answer: %d\n",lsearch);
			printf("Expected Answer: %d\n",expect);
			printf("Array Used:\n");
			printArray(A,n);
			printf("******END ERROR********\n");
			return false;
		}
			
	}
	return true;
}

//Run t tests on size n and average
float averageTime(int n, int t){
	int total = 0;
	int* X = randArray(n);
	for(int i=0; i < t; i++){
		//Pick a random number 0 to 2n (exclusive of 2n)
		int target = rand()%(2*n);
		int before = clock();
		bool t = linear(target,X,n);
		int after = clock();
		total = total + (after-before);
	}
	free(X);
	return (float)(total)/(float)(t);
}

previous

Iterative Algorithms

next

Bubble Sort