Introduction to Trees
Contents
Introduction to Trees¶
Nodes and Edges¶
Trees are one of the most commonly used Abstract Data Types. The basic idea of a tree is a very general concept. It can be used in many different ways.
The abstract concept of a tree can be defined as a collection of ordered related values. The Abstract Data Type is best described visually.
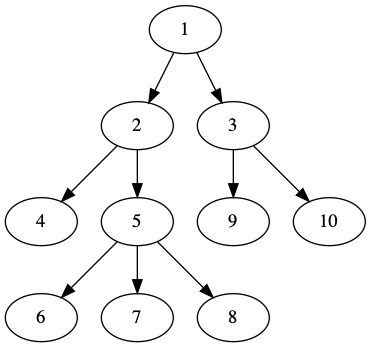
Values in a tree are stored in Nodes. In this tree, the values are integers. It is possible nodes will have a value and a label. This is helpful when we have repeated values. The tree has no repeated values, so we just need to show the values.
The tree also has Edges. An edge is an arrow drawn between two nodes. Notice that all the arrows go in the same direction. When we talk about edges we refer to them as a pair (from node, to node). In this tree, we would say there is an edge (2,4) because there is a line drawn from the edge labeled 2 to the edge labeled 4.
Basic Terminology¶
Some of the terminology about trees is based on family trees. A node’s child is a node that it is connected to by an edge. A node’s parent is the node an incoming edge comes from.
Parent: node \(x\) is node \(y\)’s parent if and only if there exists an edge from \(x\) to \(y\)
Child: node \(x\) is node \(y\)’s child if an only if there exists an edge from \(y\) to \(x\)
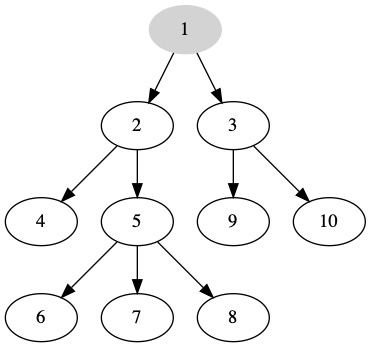
Trees always have a direction. The root or top of the tree is the first node. Is has no edges pointing to it and is normally drawn at the top of the tree. We can also define the root as the only node with no parent. The root is highlighted in grey below.
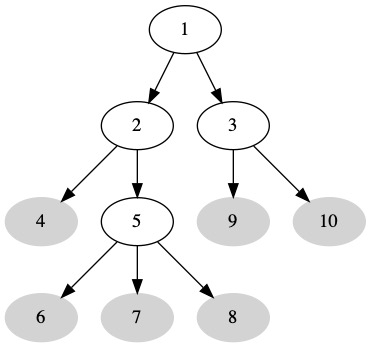
The root terminology comes from actual trees. The term leaf also comes from real trees. A leaf is a node with no children. The leaf technically has null children. These null children as normally not drawn. Sometimes they are shown to clarify an image. The leaves of the tree are show below in grey.
Node 1 has no parent. Node 7 as no children. Node 5 is a child of Node 2. Node 2 is the parent of Node 4.
If two children have the same parent they are called siblings. In this tree, Node 4 and Node 5 are siblings. They are both children of Node 2.
Root: a node with no parent
Leaf: a node with no children
Siblings: Nodes \(x\) and \(y\) are siblings if and only if they have the same parent.
Paths¶
A Path is a sequence of nodes connected by edges. In a tree, a path relates parents and children.
There exists a path from node \(a\) to node \(c\) if and only if there exists a sequence of edges \((a,x_1), (x_1, x_2), \cdots, (x_n, c)\).
Note
If \(x_1, x_2, x_3, \cdots x_k\) is a sequence of nodes in a tree such that \(x_i\) is the parent of \(x_{i+1}\) for all nodes \(1 \le i \le k\) then this sequence is a path from \(x_1\) to \(x_k\).
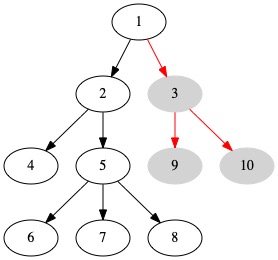
Every node has a path to itself with zero edges. It is correct to say there is a path from node \(2\) to node \(2\). No movement is needed. This path just means to stay at the same node.
The red edges show a path from node \(1\) to \(7\). The sequence of edges is \((1, 2), (2, 5), (5,7)\).
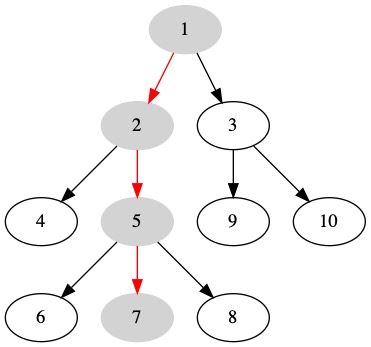
A path does not have to start at the root or end at a leaf. A path can be any sequence of nodes connected by edges. The path from \(2\) to \(6\) is shown below.
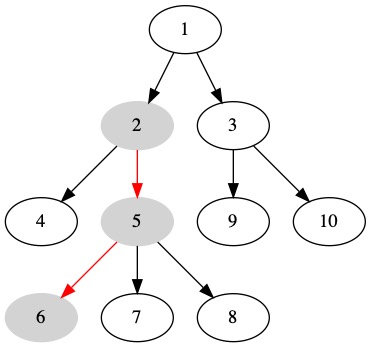
Node Height¶
The Node Height of a tree is the maximum number of edges on a path from the node to a leaf.
The Node Height of Node \(2\) is \(2\) edges. There is one leaf \(1\) edge away. There are three leaves \(2\) edges away. The maximum number of edges along a path from \(2\) to an edge is \(2\) edges.
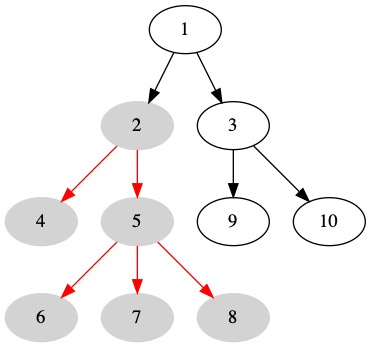
Tree Height¶
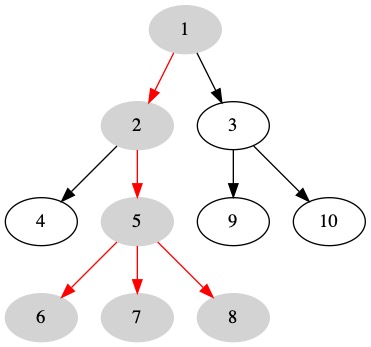
The Tree Height is the maximum number of edges on a path from the root to a leaf. This is the node height of the root.
In this tree, there are three paths from the root to a leaf that have \(3\) edges. The Tree Height is \(3\).
The paths containing \(3\) edges are highlighted in the following image.
Node Depth¶
The Node Depth is the number of edges on a path from the root to a node. The node depth of Node \(5\) is \(2\) edges. The path from the root to node \(5\) is \((1,2), (2,5)\).
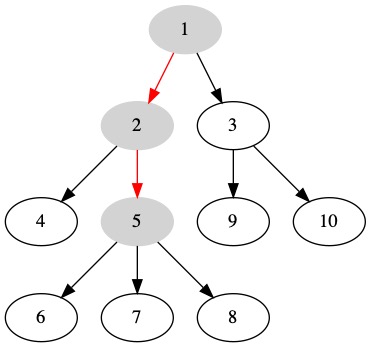
Height/Depth Summary¶
The node depth and node height of every node in the tree is given in the following table. The tree height is the node height of the root node. Notice that the tree height is also the maximum node depth.
Node |
Height |
Depth |
|---|---|---|
1 |
3 |
0 |
2 |
2 |
1 |
3 |
1 |
1 |
4 |
0 |
2 |
5 |
1 |
2 |
6 |
0 |
3 |
7 |
0 |
3 |
8 |
0 |
3 |
9 |
0 |
2 |
10 |
0 |
2 |
An empty tree is considered to have a height of \(-1\). An empty tree is a tree with no values in it.
Ancestors and Descendants¶
Returning to family trees, the terms ancestor and descendant can be defined for trees.
Node \(a\) is node \(b\)’s ancestor if and only if there exists a path from \(a\) to \(b\).
Node \(b\) is node \(a\)’s descendant if and only if there exists a path from \(a\) to \(b\).
Node 7 has the following ancestors: 7, 5, 2, and 1.

Node 2 has the following descedents: 2, 4, 5, 6, 7, and 8.

Note
A node is it’s own ancestor and descendant. This is because every node has a zero edge path to itself. If don’t want to consider this path, add the word proper. A proper ancestor or proper descendant does not include the node itself.
There is a path from node 2 to node 6. Node 6 is an descendant of node 2. Node 2 is an ancestor of Node 6.

The proper descendents of node 2 do not include node 2.
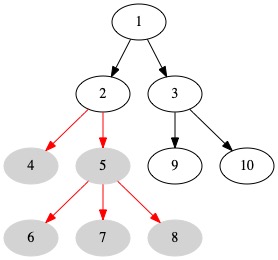
Left and Right¶
If nodes A and B are siblings and A is to the left of B in the tree then
all the descendants of A are to the left of all the descendants of B
all the descendants of B are to the right of all the descendants of A.
Node 2 and node 3 are sibling. Therefore, we know that 2, 4, 5, 6, 7, and 8 are all left of node 3. Additionally, we know that 3, 9, and 10 are all right of node 2.
Nodes to the right of 2 are colored below