Deterministic Finite Automaton
Contents
Deterministic Finite Automaton¶
A Deterministic Finite Automaton (DFA) is a state machine that follows a specific set of guidelines. Any problem that can be solved by a DFA can be solved in linear time. This means it looks at every element of its input exactly one time. This is commonly used for string matching.
Formal Definition of a DFA¶
A DFA is a 5-tuple. This means it is built from 5 components. Formally we would write \(M=\left( Q, \Sigma, \delta, q, F\right)\).
The five components of the DFA are described below.
\(Q\) is a finite set of states
\(\Sigma\) is a finite set of symbols called the alphabet
\(\delta\) is set of transitions between states.
\(q\) is the start state.
\(F\) a set of accept states. \(F\) is a subset of \(Q\).
A DFA is said to accept an input if it exists in an accept state.
To understand these components, we will look at a simple example.
Toll Booth Gate¶
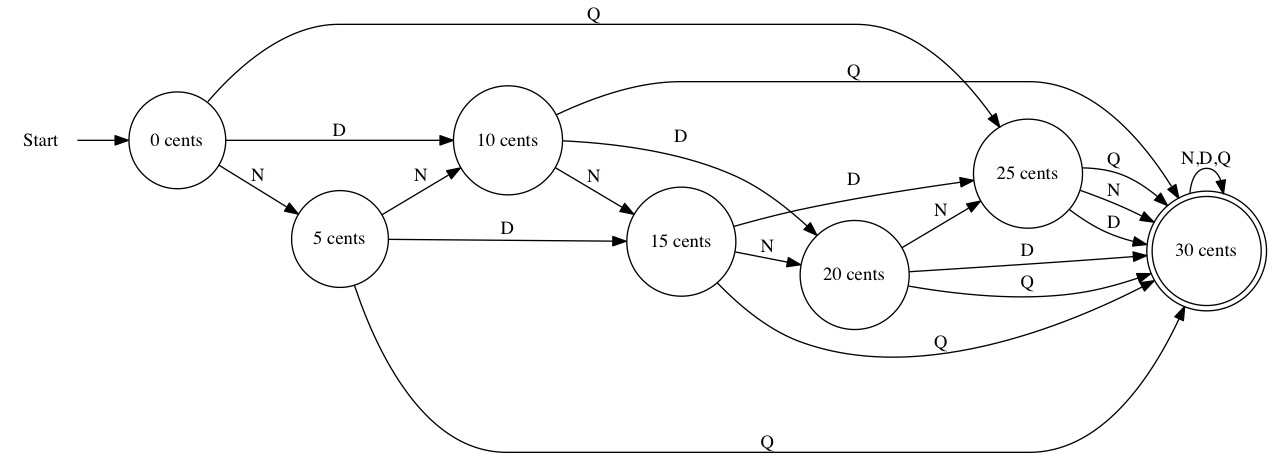
Imagine we want to model a Toll Booth Gate. A car drives up to the toll both. They put change into the machine. When they put enough change in, the gate opens. Once the gate goes back down again, the toll booth starts from the beginning.
For simplicity, we will only accept three kinds of change: nickles, dimes, and quarters. The gate will open when it hits 30 cents. If extra money is put in, the toll booth gets to keep it.
The alphabet of the DFA is the finite set of symbols it can accept. Our toll booth can only accept nickles, dimes and quarters. We will use shorthand symbols for each.
N is a nickle worth 5 cents
D is a dime worth 10 cents
Q is a quarter worth 25 cents
Our alphabet is \(\Sigma=\{N, D, Q\}\).
The toll booth’s states are based on the amount of money put in. The amount can be aware from 0 to 30 cents. Over 30 doesn’t need another state. Once we hit 30 the gate opens. Once the gate closes, we start the DFA. We also don’t need every possible value. Since the toll booth does not accept pennies, not every amount is reachable.
The set of states the toll booth can be in is given below. \( Q=\left\{S_0, S_5, S_{10}, S_{15}, S_{20}, S_{25}, S_{30} \right\} \)
Our transitions are determined by adding new coins. The transitions can be described by a table. The rows of the table lists the states. The columns list the alphabet. Each value in the table is the state to transition on.
Current State |
N |
D |
Q |
|---|---|---|---|
\(S_{0}\) |
\(S_{5}\) |
\(S_{10}\) |
\(S_{25}\) |
\(S_{5}\) |
\(S_{10}\) |
\(S_{15}\) |
\(S_{30}\) |
\(S_{10}\) |
\(S_{15}\) |
\(S_{20}\) |
\(S_{30}\) |
\(S_{15}\) |
\(S_{20}\) |
\(S_{25}\) |
\(S_{30}\) |
\(S_{20}\) |
\(S_{25}\) |
\(S_{30}\) |
\(S_{30}\) |
\(S_{25}\) |
\(S_{30}\) |
\(S_{30}\) |
\(S_{30}\) |
\(S_{30}\) |
\(S_{30}\) |
\(S_{30}\) |
\(S_{30}\) |
If the machine is currently in state \(S_{10}\), that means it has 10 cents. If we insert a nickel, then the machine should have 15 cents. If we look at row \(S_{10}\) of the table and move to column \(N\) we need the value is \(S_{15}\). This shows that inserting the nickles moves the machine to 15 cents.
We call this table \(\delta\) or the transition table.
Lastly, we need to know the start and accept states. The machine always starts with no money. The start state is \(q=S_0\). We are only allowed to have one start state.
The machine accepts if it reaches 30 cents. We are allowed to have multiple accept states. We only need one \(Q=\{S_{30}\}\).
What it means to accept is ambigious. This is something that needs to be decided by the designer. In our case, accept means open the gate. In general, accept just means we succeeded at whatever our task was. Whatever we were looking for, we have found it.
If the machine exists and it is not in an accept state, we say it rejected. Whatever it was supposed to accomplish, it did not. In our example, rejection means the gate doesn’t open.
We can draw the state machine. This picture actually shows everything we need to know about the DFA.