Queues
Contents
Queues¶
Have you ever been in line at a grocery store? The first person to get it line is served first. New people come and get in the end of the line.
This is a problem computers have to deal with all the time. Imagine you go to a website to buy tickets for a concert. There might be many people all buying tickets, but they need to be given out in the order of arrival.
The Queue is a first-in-first-out Data Structure. It allows values to be ordered based on their arrival into a line.
Queue Abstract Data Type¶
The line at a cashier is a Queue.
First come, First Served.
You arrive at the back of the line.
The cashier checks out the front of the line.
The queue needs the following abilities.
Create a new line
Check if the line is empty
Add to the end of the line
Remove from the front of the line
Look at the front of the line
This can form the foundation for an Abstract Data Type. The Abstract Data Type needs the following functionality.
Create a new queue
Check if the queue is empty
Enqueue a new value onto the back of the queue
Dequeue the value from the front of the queue
Look at the front value on the queue
This gives us a conceptual model for the queue. We can build it using a Linked List of Nodes. Just like the stack!
Queue Data Structure¶
We need to know where the front and back of the queue is. We will call the front the head. We will call the back the tail.
//A Queue data structure
struct Queue {
Node* head; //The front
Node* tail; //The back
};
To make the Data Structure useful, we need to implement operations to use it.
Queue Operations¶
The queue needs to be able to do everything our Abstract Data Type described.
newQueue()- Create a new empty queueisEmpty(Q)- Determine if queueQis empty or notenqueue(v, Q)- Add valuevto the back of queueQfront(Q)- Look at the value at the front of queueQdequeue(Q)- Remove the top value of queueQ
To create a new queue we need to allocate a pointer to the structure. We just point the head to nil and tail to nil.
Function newQueue()
Allocate memory for a Queue, store pointer in Q
Make Q's head = nil
Make Q's tail = nil
Return Q
End Function
To determine if the queue is empty, we just need to see if the head is pointing to the null value or not. Each language has its own symbol for null.
Function isEmpty(Pointer to Queue named Q)
Return Q's head == Null Value
End Function
To check the front element in the queue, we just need to look at the value of the head node. We return -1 if the list is empty to avoid error checking. In practice, throwing an error would be important for production code.
Function front(Pointer to Queue named Q)
If Q's head is Null then
Return -1
End If
Return Q's head's value
End Function
To enqueue a new value, we need to first make a node. If the queue is empty, the new node is both the head and the tail. If the list already has elements, we just update the tail.
Function enqueue(integer v, Pointer to Queue named Q)
Let newNode be a pointer to a new node
newNode's value = v
newNode's next = nil
If Q's head is Null then
//This is the first value
Q's head = newNode
Q's tail = newNode
Else
//Add to the end
Q's tail's next = newNode
Q's tail = newNode
End If
End Function
To deqeue a value, we just move the head of the queue forward one pointer in memory. If this emptied the queue, we need to update the tail as well.
Function dequeue(Pointer to Queue named Q) {
If Q's head is Null then
Return //Nothing to do
End If
//Move forward 1 space
oldHead = Q's Head
Q's head = Q's head's next
free the oldHead
//We just erased the tail
If Q's head is Null then
Q's tail = Null
End If
End Function
Queue Runtimes¶
All queue operations are all constant time. This means if we solve a problem with a queue we don’t have to worry about the data structure slowing down out program. Each operation will run in constant time.
Method |
Runtime |
|---|---|
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(1)\) |
|
\(O(1)\) |
The queue is a low level data structure. It is frequently used as part of much bigger algorithms. Having a constant run time means it will be very efficient to use.
Print Queue¶
You have probably used hundreds of queues without realizing it. Every time you send a file to a printer, it gets placed in a queue. A printer can only print one thing at a time, but lots of people can send things to print. They get put into a queue and handled in order.
The printer starts with an empty queue. A networked printer would probably be in sleep mode at this point.
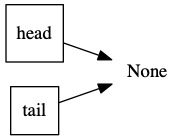
Ted sends file1.pdf to the printer. The printer wakes up and gets to work.
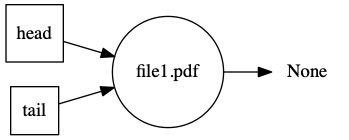
Before the printer is done, Mike sends file2.pdf to the printer. A line is starting to form.
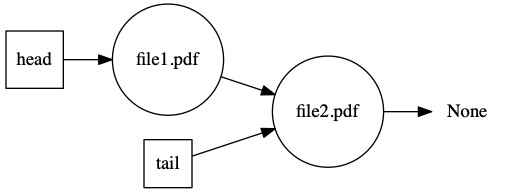
The first document still isn’t done. Alice sends file3.pdf to the printer.
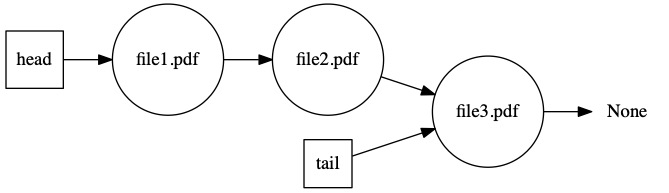
The first file finally finishes. It gets dequeued from the printer queue. The next file starts printing.
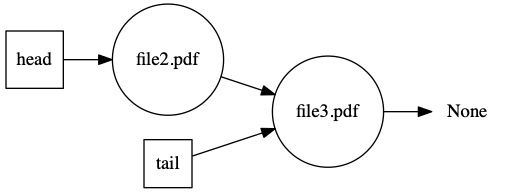
The printer makes it to the last file it needs to print. Notice that the head and tail are both pointing to the same file.
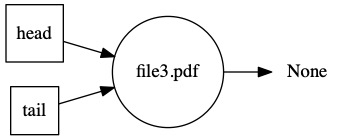
Once the last file prints, the queue is empty again. The printer can go into sleep mode until new data enters the queue.