Heaps¶

Priority Queues¶

A Priority Queue is a abstract data type designed to store things based on their priority. It is similar to a queue, except higher priority items get to the front of the line faster.

The priority queue you are probably most familiar with is a hospital emergency room. Unlike the grocery store, the first person to get in line might not be the first person served. The emergency room gives each patient a priority based on how bad their medical issue is. You may be waiting a long time for a minor issue if an ambulance arrives. That person will jump in front of everyone else because their problem has a higher priority.

A priority queue is a partially ordered data structure. We need to know who the next person is right away. We don’t really care who is tenth in line. We focus our energy on keeping track of the highest priority items.

Priority Queues have many low level functions on computers.

Deciding which program runs on the processor next
Deciding which program gets to use a piece of hardware next (network port, hard drive, printer)
Managing network bandwidth (VoIP takes priority over emails)

On a computer, we normally define highest priority in an unexpected way. Think about binary again. The largest number on an 8-bit system is 255. On a 32-bit system, the largest number is 4,294,967,295.

What number do we give the highest priority item? The easiest answer is zero! No matter how many bits the processor uses, zero is always the smallest unsigned integer. We can make zero the highest priority and know our priorities will be right on any processor.

On computers we traditionally assign

0 to be the highest priority (normally the Operating System)
large numbers to lowest priority

This way we can design algorithms that work on any system.

The idea of a priority queue is some way to organize items based on the their priority. There are many ways to try and build this. The most common is called the heap.

Heap¶

A Heap is an implementation of a Priority Queue. The Heap is a data structure. The heap is a kind of binary tree. It is partially ordered. We will create a min-heap, where the root is the smallest value. These concepts can be easily converted into a max-heap. The heap has two properties that will hold true.

The root node is the smallest value
A child is always greater than or equal to it’s parent

Notice that there is no relationship between siblings. We don’t care about which sibling is larger or smaller, as long as the parent is smaller (or equal).

Since a heap is partially ordered, we can make sure it never has gaps in the tree. This means we can store it in an array. To store the tree in an array, we need to know three things.

The max size of the array.
The current size of the array.
The data stored in the array.

An array is a fixed space of memory. When we allocate an array, we have a certain number of spaces. This is the maximum size the heap can reach without having to allocate new memory. We might not actually have every space filled. The current size tells us how many spaces are filled with values.

Since we are using an array, we don’t have pointers for left child, right child, or parent. We need formulas to determine where they are in the array.

The parent of the node at index \(i\) is at index \(\left \lfloor (i-1)/2 \right \rfloor\).
The left child of the node at index \(i\) is at index \(2*(i+1)-1\).
The right child of the node at index \(i\) is at index \(2*(i+1)\).

These formulas allows us to move around the tree as if we had pointers. If the index \(i\) is 0, then we know we are at the root. If a left child or right child has an index that is greater than or equal to the current size, then that position is empty.

When the heap starts, all the spaces in the array are empty. When a new element is inserted, we always put it in the next available space in the array. We also increase the current size by 1. When we insert a new element, we can’t be sure it won’t brake the rules of the heap.

Once a new value is inserted, we check that the heap property holds. Is the new child we inserted actually greater than or equal to it’s parent? If it is, then we put in it the right place.

If it is not, then the heap is no longer valid. We need to fix the heap. To do this, we swap the value with its parent. Since the parent was clearly larger, this fixes the local area of the heap. It might not fix the entire heap. The process of upheaping is when we repeatedly swap children with their parents until the heap is fixed.

The following animation shows a series of values being inserted into the heap. If the heap is not correct after the insert, then upheaping is used to fix the heap.

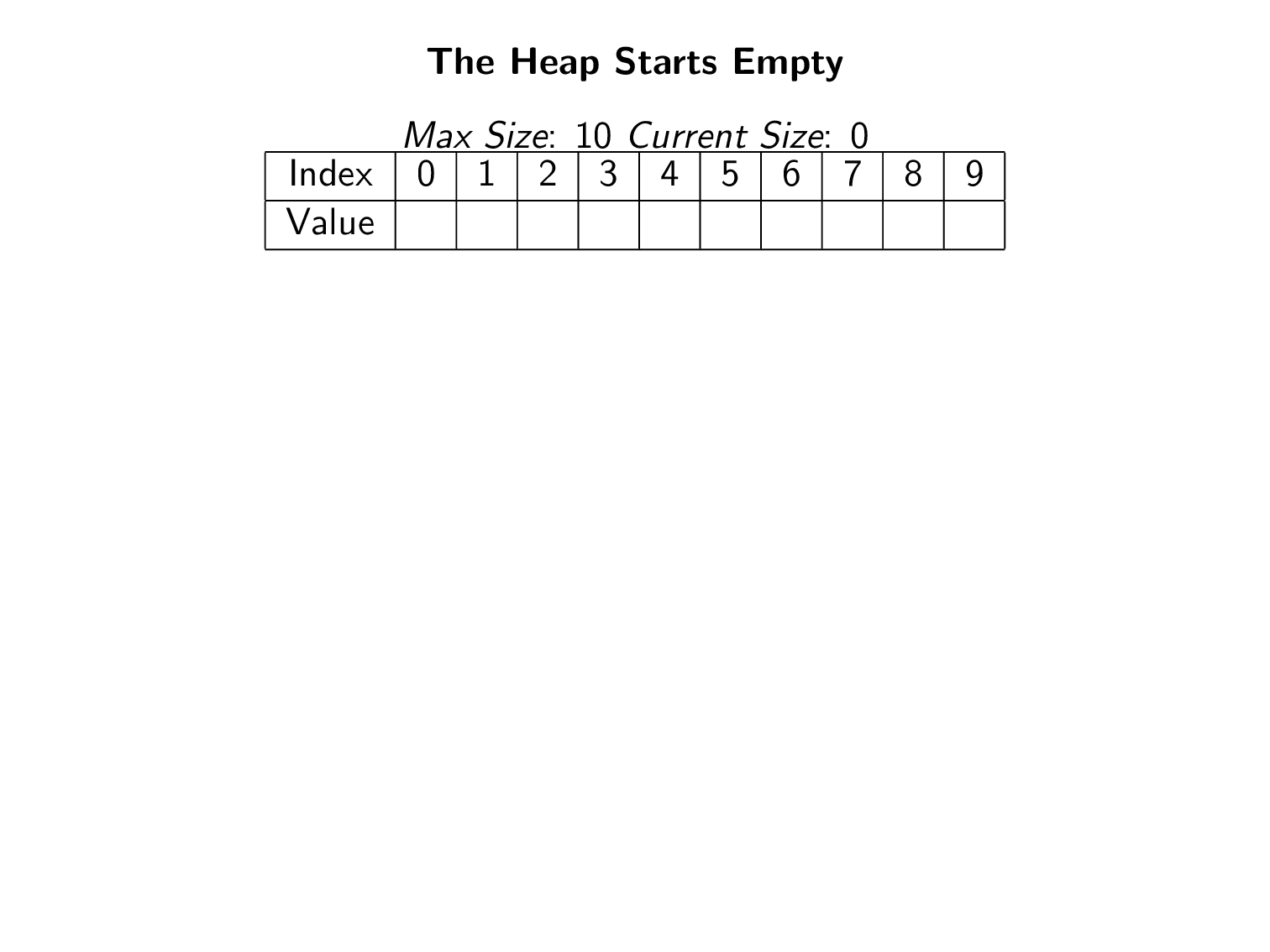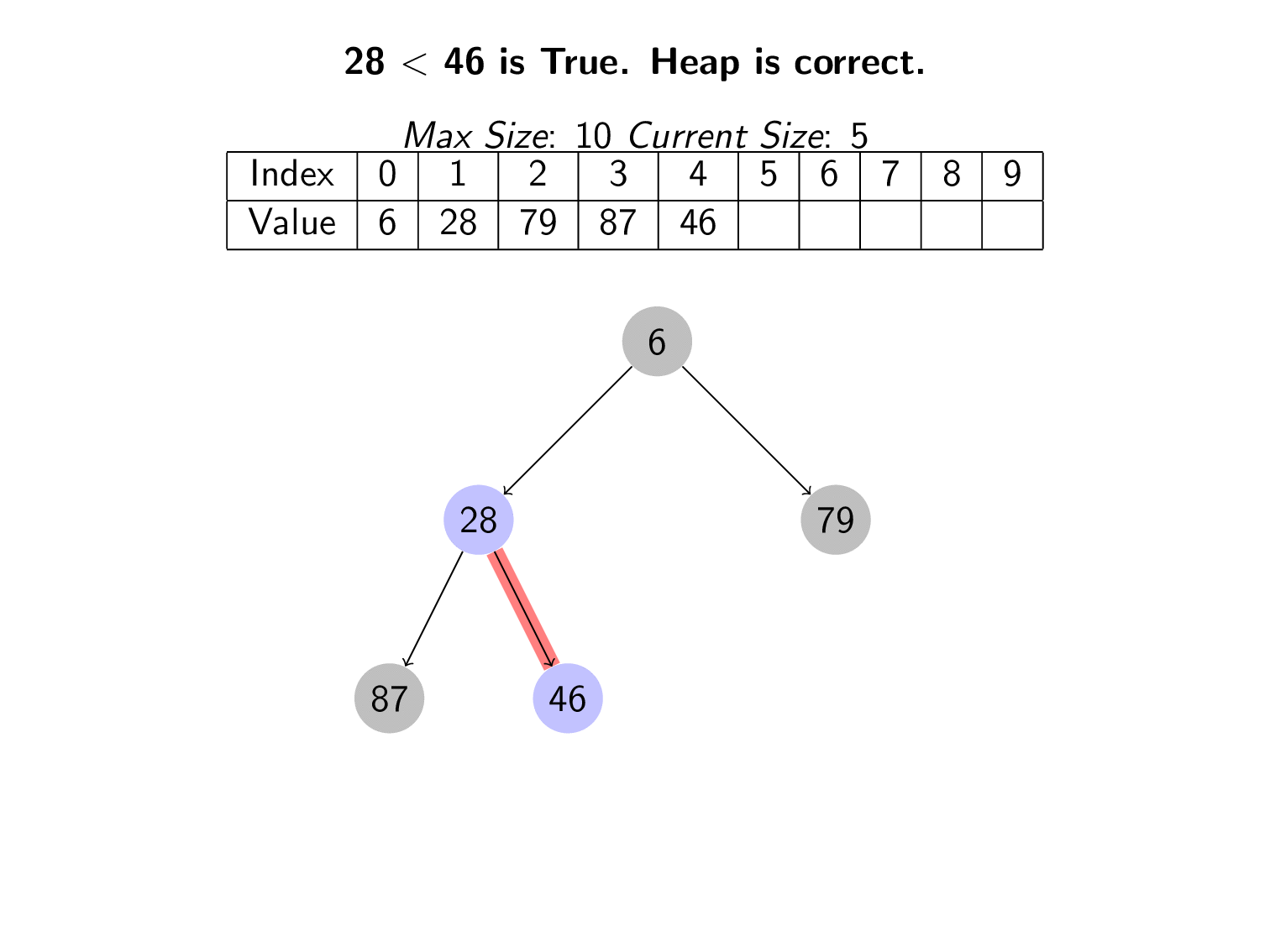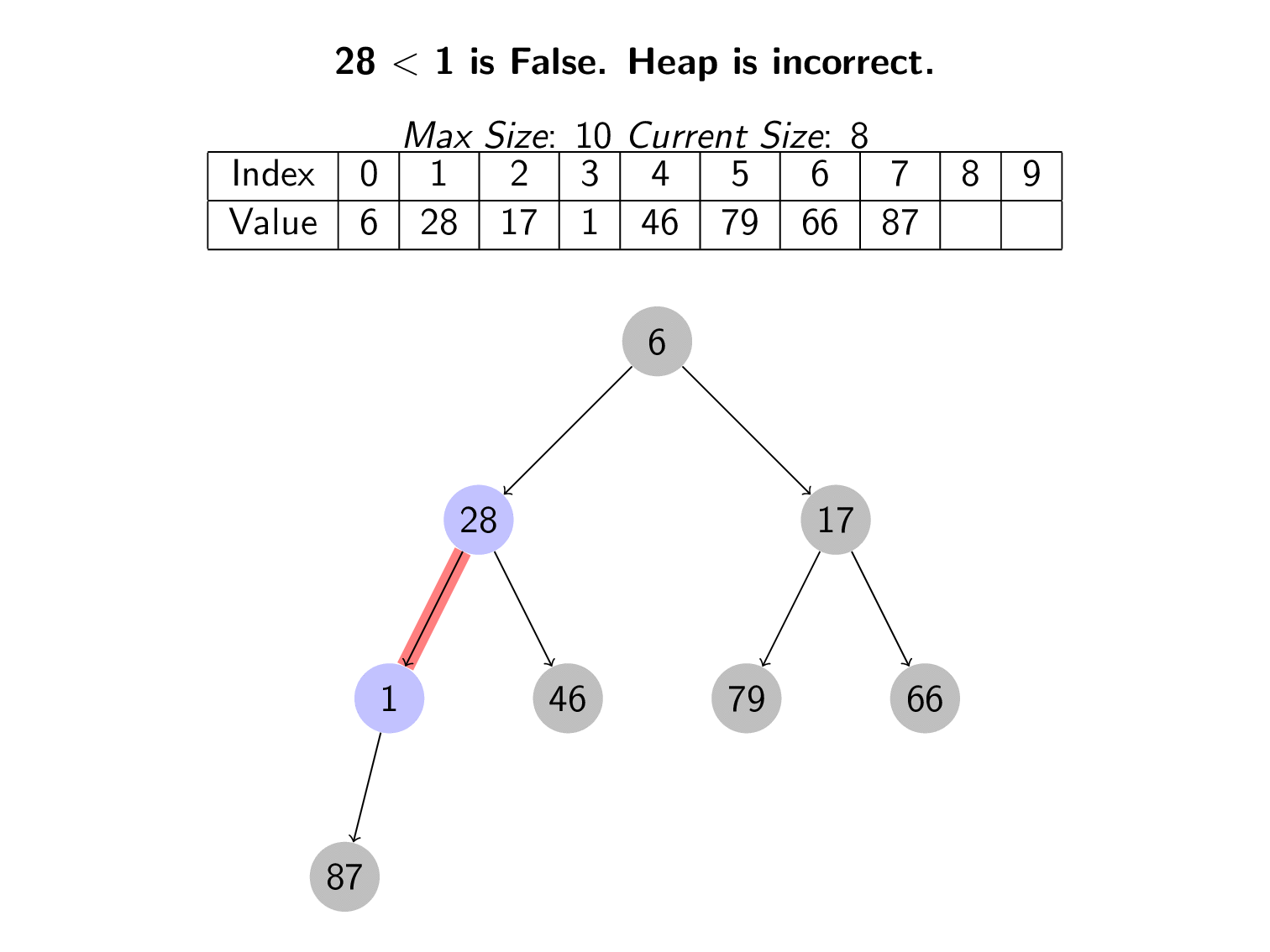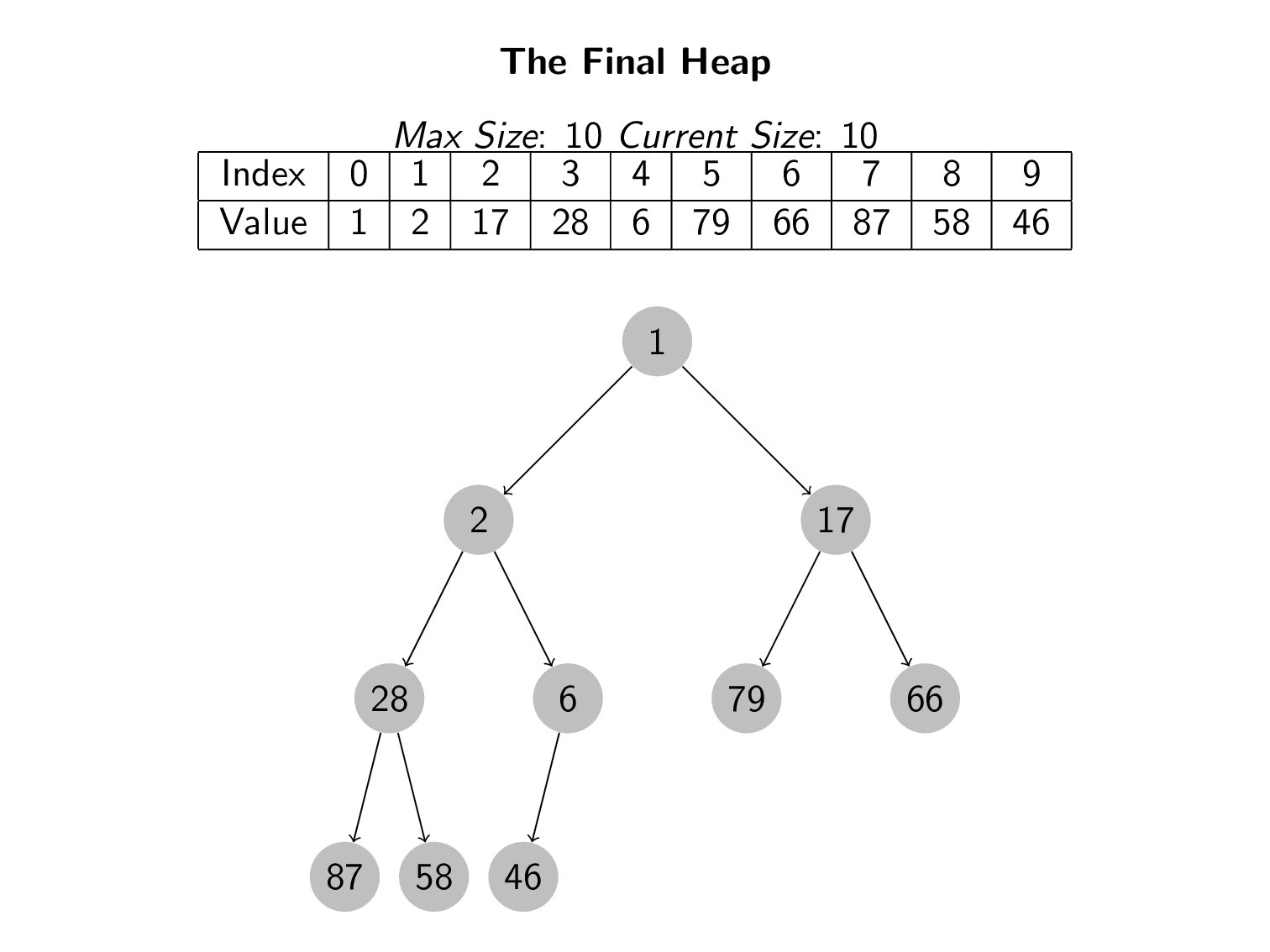
Inserting Values Into a Heap

By following this pattern, the value with the lowest value (highest priority) will always move to the top of the tree. The minimum value is at index 0 of the array.

We can insert values into the heap and the smallest value will always move to the top of the tree. These easily provides the first part of a priority queue. Now that the highest priority item has moved to the top, we need some way to remove it.

It would be very easy to remove a value from the end of the array. We could just decrease the current size by 1. Sadly, we need to delete the root. The most important feature of a heap is quickly finding the minimum. Once we find it, we generally need to delete it.

We can take advantage of the last element being easy to remove. To delete the minimum from the heap, we swap it with the last element in the heap. Then we decrease the current size by 1. We have removed the root, but we might have broken the heap properties.

We use a process called downheap to fix the heap. We compare the newly swapped root with it’s two children. It should be smaller than both its children. If is it not, we can swap it with the smallest child. We repeat this process until the heap properties hold again.

The following animation shows all the elements being deleted from the heap. Notice that each time a swap breaks the heap properties, downheaping is used to repair the heap.

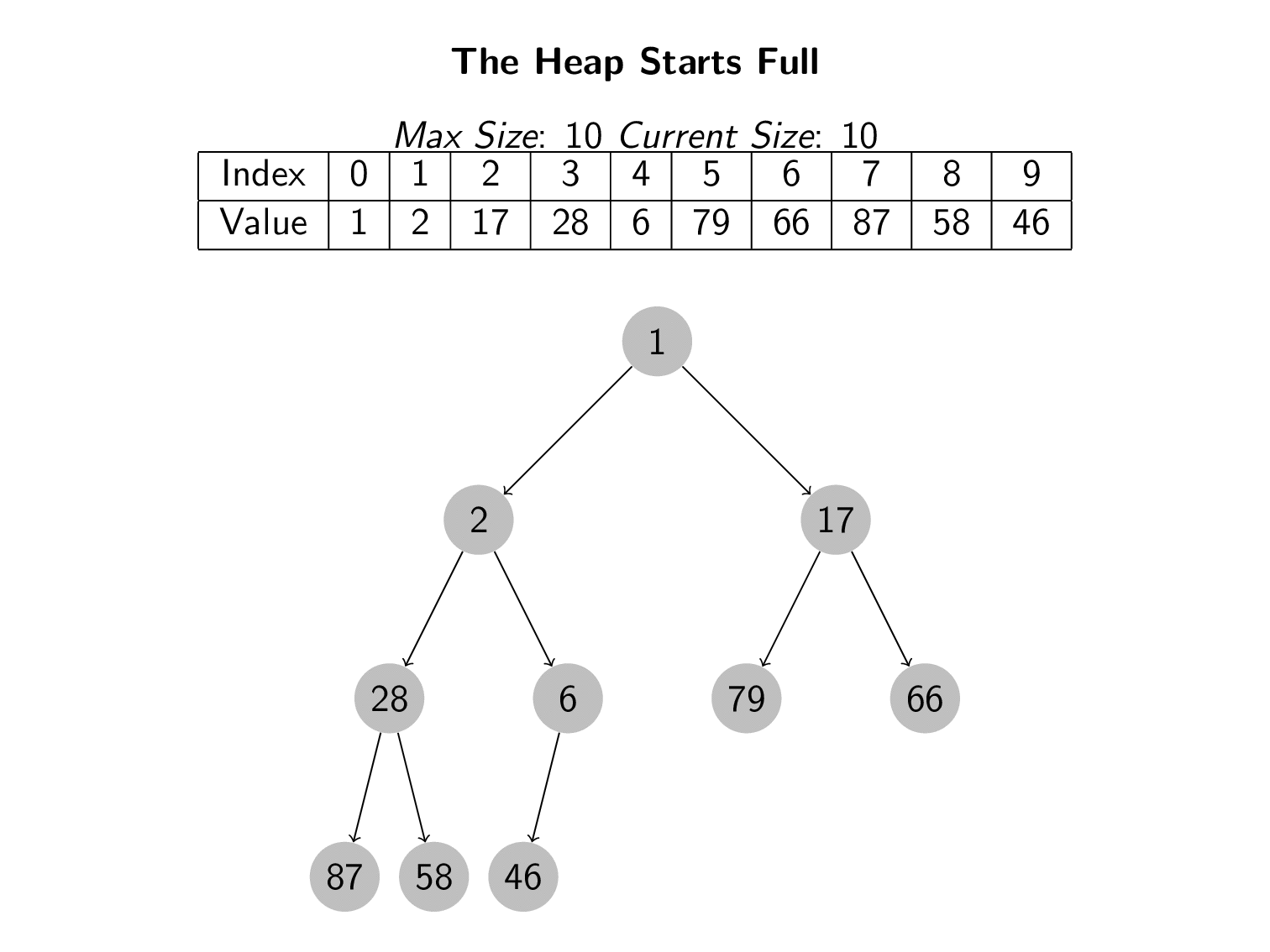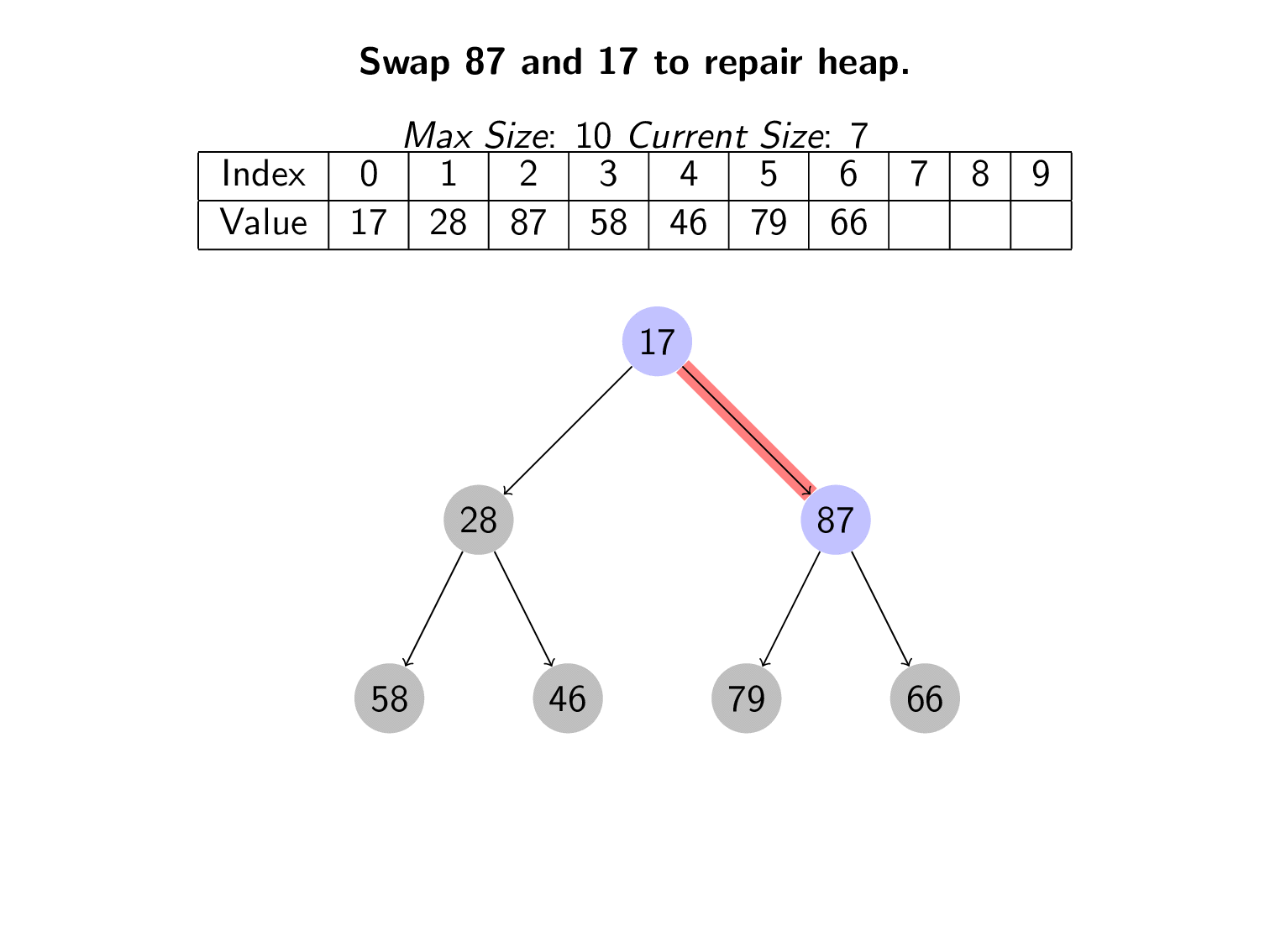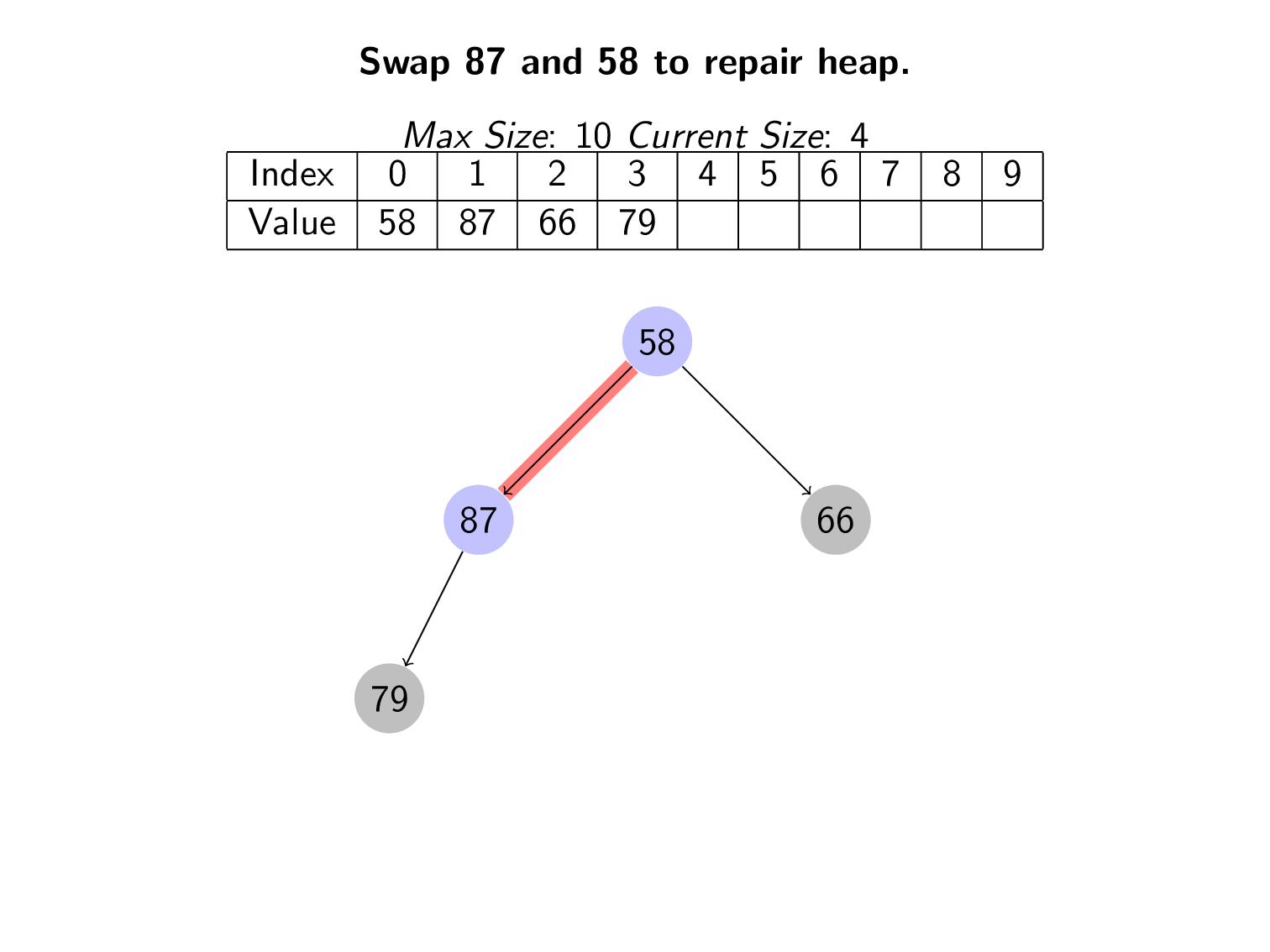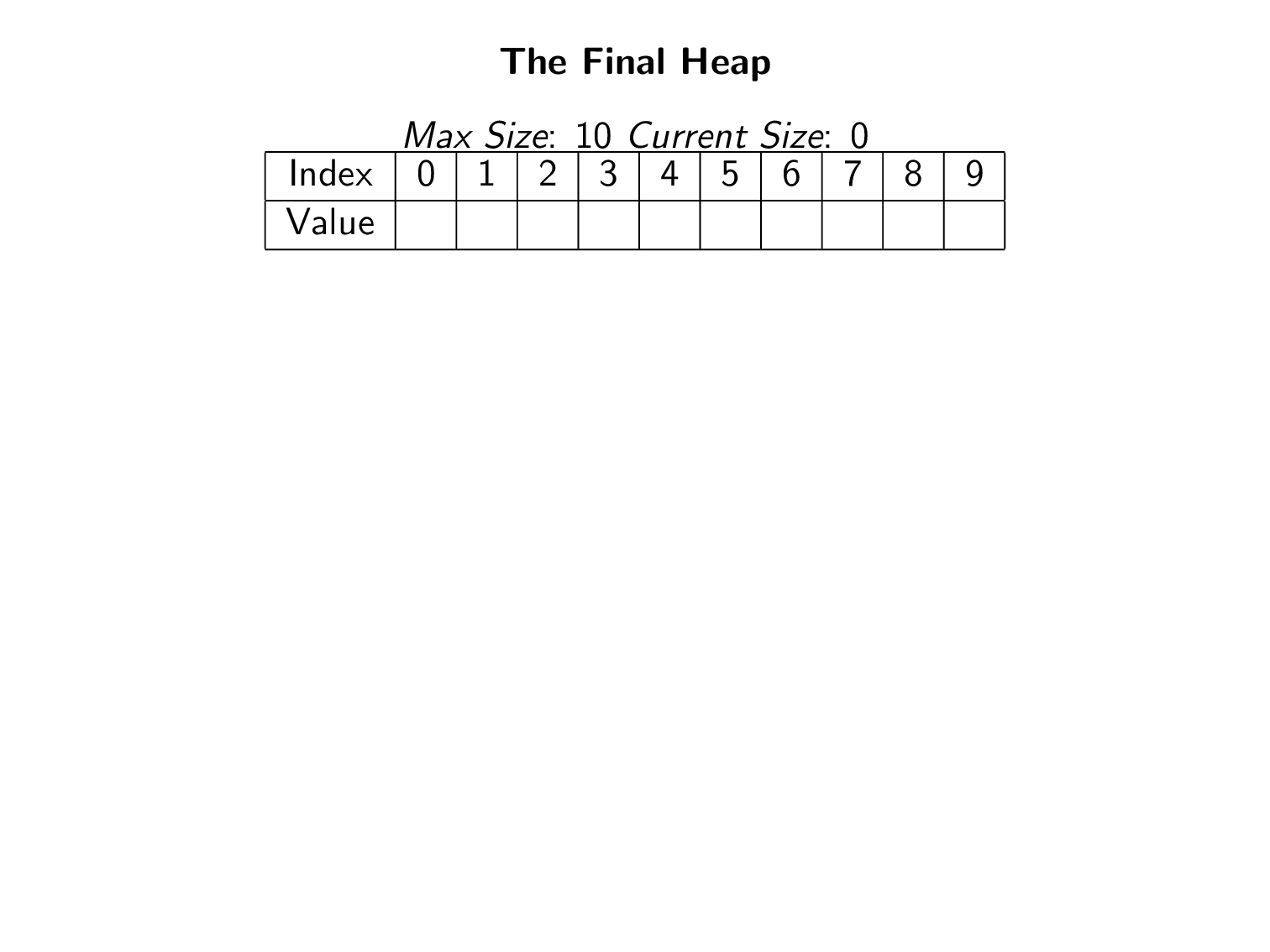
Deleting Values from a Heap

Using a combination of swapping and downheaping, we can retain the heap properties. After deleting the minimum, the new minimum will end up at the root position. This meets all the requirements of the priority queue. The value with the highest priority is always at the top.

Implementation¶

To implement the heap, we need a structure. We need a pointer to the array storing all the data. We also need to know the max size of the array and the current size.

//Heap is a classic min-heap stored using an array
structure Heap {
    //A pointer to the array of values
    ArrayPointer data
    //The max number of values array can store
    int maxSize
    //The current amount of values
    int currentSize
}

We need to initalize the values when we create a new heap. The function MakeHeap creates a new empty heap. We require the user to set an initial capacity.

//MakeHeap Allocates a new empty heap
Function MakeHeap(int capacity)
    Let H = allocate(Heap)
    H's data = allocateIntArray(capacity)
    H's currentSize = 0
    H's maxSize = capacity
    Return H
End Function

We need to be able to determine if the heap is empty. This is easy. We just need to look at the current size. A current size of zero means the heap is empty.

//Empty returns true if the heap is empty
Function Empty(Heap Pointer H)
    return H's currentSize == 0
End Function

One of the most important features of the heap is finding the minimum. This is also trivial, it always lives at index 0. We return 0 when the heap is empty, but this might be situation where throwing an error would be helpful.

//Min returns the smallest value in the heap or 0 when empty
Function Min(Heap Pointer H)
    If Empty(H) then
        return 0
    End If
    //The min is always at the root
    Return H's data[0]
End Function

To insert a value, we put it in the next available space in the array. Then we need to upheap until the heap properties are restored. This implementation of Insert will resize the array if we run out of space. This is a costly action and should be avoided when possible.

//Insert value x into heap H
Function Insert(int x, Heap Pointer H)
    If H's currentSize == H's maxSize then
        expand(H)
    End If
    H's data[H's currentSize] = x
    H's currentSize++
    upheap(H, H's currentSize-1)
    Return
End Function

If we can insert values, we also need to be able to delete them. A traditional heap only allows the minimum to be deleted. To delete the min, we swap it with the last element and decrease the size of the array. If this causes the heap properties to be broken, a call to downheap will repair the heap.

//DeleteMin deletes the root of the heap
Function DeleteMin(Heap Pointer H)
    //Nothing to do
    If Empty(H) then
        Return
    End If
    //Swap Root and last element
    swap(H, 0, H's currentSize-1)
    //Decrease size
    H's currentSize = H's currentSize - 1
    //Fix the heap starting at root
    downheap(H, 0)
End Function

There are a number of helper functions required for this data structure. We need to be able to find the parent index.

//The parent of node i is at index floor((i-1)/2).
Function parent(int i)
    //Root has no parent
    If i == 0 then
        Return -1
    End If
    //Reminder: Integer division
    Return (i - 1) / 2
End Function

We also need to be able to find the index of the left and right children.

//The left child of node i is at (i+1)*2-1=2i+1
Function leftChild(int i)
    Return 2*i + 1
End Function

//The right child of node i is at (i+1)*2=2i+2
Function rightChild(int i)
    Return 2*i + 2
End Function

We will frequently need to swap values in the array. Most languages provide some shortcut for this, but we will implement it here. This is the most language agnostic solution.

//Swap Two Values in the Heap's data array
Function swap(Heap Pointer H, int i, int j)
    Let temp = H's data[i]
    H's data[i] = H's data[j]
    H's data[j] = temp
    Return
End Function

We have already seen that Insert might need to resize the array. This requires allocating a new array. We then copy all the values to the new area of memory.

//Expand the size of the array to fit more elements
Function expand(Heap Pointer H)
    Let newSize = 2 * H's currentSize
    Let newData = allocateIntArray(newSize)
    //Copy Data to new memory
    For i = 0, i < H's currentSize, i++ do
        newData[i] = H's data[i]
    End For
    Let oldData = H's data
    H's data = newData
    H's maxSize = newSize
    Free memory from oldData
    Return
End Function

The most unique functions for the heap are named after it, upheap and downheap.

Upheap starts the the index of the value we inserted. If that index has no parent, then we can stop. The value is already the root, so the heap must be correct. Otherwise, we need to find out that value of our parent. If it is larger than the target index, we swap the two values. This will fix the local area of the heap, but there might be more problems. By calling upheap recursively after the swap, we continue swapping until the heap is repaired.

//Upheap value at index i until heap is valid again
Function upheap(Heap Pointer H , int i)
    //Determine the parent
    Let p = parent(i)
    //Already at root
    If p < 0 then
        Return
    End If
    //Determine parent's value
    Let pVal = H's data[p]
    //If less than value at i, then heap valid
    If pVal <= H's data[i] then
        Return
    End if
    //Otherwise Swap with parent
    swap(H, i, p)
    //Continue to swap till valid heap
    upheap(H, p)
    Return
End Function

The downheap command is always called after a delete. It starts on the index of the swapped value. If the target index \(i\) has no children, then there is nothing to downheap and the heap properties must hold. Otherwise, we need to determine which of the two children of the node contain the smallest value. This is split into it’s own function. If the parent is larger than its smallest child, then need to trade places. After the swap, we downheap again. The process continues until the heap properties hold again.

//Starting at index i, move value down until
//the heap is valid again
Function downheap(Heap Pointer H, int i)
    //Determine Location of Children
    Let leftIndex = leftChild(i)
    Let rightIndex = rightChild(i)
    //Part 1: No children, nothing to do
    If leftIndex >= H's currentSize then
        Return
    End If
    //Part 2: Determine Smallest Child Node
    //Create a variable to store smallest child index
    Let minIndex = pickSmallerChild(H, leftIndex, rightIndex)
    //Part 3: Repair Heap
    //If the smallest child is less than value at i, swap
    If H's data[i] > H's data[minIndex] then
        swap(H, i, minIndex)
        downheap(H, minIndex)
    End If
    Return
End Function

To keep the code easy to read, we made a special function for finding the minimum index of the node’s children. If there is no right child, the left child wins by default. Otherwise, we need to compare the two values and select the smallest.

//Given two indexes, pick the smaller of the two
Function pickSmallerChild(Heap Pointer H, int leftIndex, int rightIndex)
    //Variable to store return value
    int minIndex
    //If no right child, left is smaller
    If rightIndex >= H's currentSize then
        //Left is smaller
        minIndex = leftIndex
    Else //With two children we need to compare
        //Decide which is smaller
        If H's data[leftIndex] < H's data[rightIndex] then
            minIndex = leftIndex
        Else
            minIndex = rightIndex
        End If
    End If
    Return minIndex
End Function

Analysis¶

Most of the functions we have created have no loops. This makes their runtime fairly straightforward. The biggest memory usage is the heap array taking up \(O(m)\) where \(m\) is the max capacity of the array. All the other variables needed contribute just \(O(1)\) extra memory.

The following functions all have constant runtime.

Function	Runtime
`MakeHeap`	\(O(1)\)
`Empty`	\(O(1)\)
`Min`	\(O(1)\)
`parent`	\(O(1)\)
`leftChild`	\(O(1)\)
`rightChild`	\(O(1)\)
`swap`	\(O(1)\)
`pickSmallerChild`	\(O(1)\)

The expand function runs in linear time based on the capacity of the heap. If the programmer allocates a heap of the correct size, this function will never run. Since it doubles the size of the array, it will be called infrequently. A process called Amortized Analysis can be used to show that these resizes will happen infrequently and average to \(O(1)\). For now, will be just ignore expand in our analysis of other functions.

Function	Runtime
`expand`	\(O(\text{maxSize})\)

The Insert function is constant time until it calls upheap. How many times will upheap need to swap? Each time it swaps, it moves the value up one level in the tree. This means the maximum number of times upheap can be called is the height of the tree. In the worst case, we start at the bottom and go all the way to the root. The tree is a balanced binary tree, so its height is \(\log_2(n)\) when there are \(n\) elements in the tree.

Function	Runtime
`Insert`	\(O(\log_2(n) )\)
`upheap`	\(O(\log_2(n) )\)

The DeleteMin and downheap functions have a similar relationship. The DeleteMin function is constant time except the call to downheap. The downheap function’s worst case is to start at the root. With each swap, it moves the value down one level in the tree. In the worst case, downheap stops when it reaches a leaf position. If the tree has \(n\) nodes, this means it will recursively execute at most \(O(\log_2(n))\) times.

Function	Runtime
`DeleteMin`	\(O(\log_2(n) )\)
`downheap`	\(O(\log_2(n) )\)

The upheap and downheap functions are the primary drivers of the data structure’s runtime. Every time we need to insert or delete a value, we might need to do \(O(\log_2(n))\) work to repair the heap.

Heap Sort¶

If we insert a bunch of elements into a heap, we can sort them. The minimum will be at the root of the tree. If we delete it, a new minimum will replace it. If we just keep deleting, we will get all values in order from smallest to largest. This forms the basis for a sorting algorithm.

Insert all values to sort into heap
Delete all values from the heap

Every time we delete a minimum, we just need to put it in the right place in the original array. The algorithm is given below.

//HeapSort Sorts array A with size given using a heap
Function HeapSort(Array A, int size)
    Let H = MakeHeap(size)
    //Insert all Elements
    For i = 0, i < size, i++ do
        Insert(A[i], H)
    End For
    //Delete All Elements
    For i = 0, i < size, i++ do
        A[i] = Min(H)
        DeleteMin(H)
    End For
End Function

To sort an array with \(n\) elements, we need to call insert \(n\) times. We will never have to resize the array because our capacity is known. Each insert will have a runtime of \(O(\log_2(n))\). That means inserting \(n\) elements will have a runtime of \(O(n \log_2(n))\).

Next, we need to delete all the values. Deleting each value also takes \(O(\log_2(n))\). We need to delete all \(n\) values, which means the entire delete loop will take \(O(n \log_2(n))\).

Putting the two together, our entire sort takes

\( \begin{align} O(n \log_2(n)) + O(n \log_2(n)) =& O(2n \log_2(n)) = O(n \log_2(n)) \end{align} \)

This is the same runtime class as Quick Sort and Merge Sort. In practice, the implementation of a heap described here probably won’t compete well with Quick Sort. It is designed to solve the Priority Queue problem, so it can do more than sort. If you only need to sort with the heap, you could optimize the code, but it would no longer work as a Priority Queue.

Algorithmic Foundations of Computer Science

Heaps

Contents