Heap Memory
Contents
Heap Memory¶
A program stores data in three different places. How a variable is created will depend on what type of memory you are using.
Three types of memory:
Static Memory
Stack Memory
Heap Memory (also known as Free Storage)
The first type of memory is Static Memory. This is memory that can be statically assigned at compile time. For example, if you have a global variable. The compiler knows the global variable exists and is needed for the entire life of the program. It can allocate space for this variable during compile time. The amount of space will never change. The variable also stays in memory from the moment the program starts until it exists.
The second type of memory is Stack Memory. This is the memory that is allocated for functions. It is used for any local variables or function parameters. This memory is allocated when the function is called. When the function exists, this memory is freed again. The memory’s usage is directly linked to the usage of the function that it is in. The area in while a local variable is needed is called scope. Variables can have scope that is even smaller than a function. These are still stored in the Stack Memory. The space for the memory is allocated when the variable comes into scope. When the variable is no longer needed, it is removed from Stack Memory.
The third type of memory is Heap Memory. This is memory the program requests as it executes. This memory is not assigned to a variable name. It can only be accessed using a pointer. Any part of the program with a pointer to the value can access it. This memory must be freed by the program or it will not be released. The advantage is the programmer can control when the memory is created and destroyed. This will allow us to create Data Structures that use as much memory as needed.
The basic memory of a C program is shown below.
| Text |
| Data |
| Heap |
| Empty Memory |
| Stack |
The lowest memory address starts with what is called the text of the program. This is the compiled version of your source code. The actual code of the program that is being executed. Next is the data. This is things like global variables and constants. Things the compiler can plan on the memory for. Then there is a large block of empty memory. When Stack Memory is needed, the values start at the highest memory address and work their way down to the lower addresses. The Heap Memory starts right after the data. It grows up from the lower address to the higher ones as you request memory. Since each grows into the empty memory area, they can overflow each other. If you allocate enough Heap Memory, it will reach the Stack Memory and start overwriting your local variables. Likewise, if you put enough local variables in Stack Memory it will eventually grow far enough to overwrite the Heap Memory. Most operating systems will catch these errors and crash the program when it happens.
Local Memory Example¶
First let’s look at an few of memory usage that do not access the heap. The following is a short C program that computes factorials using a loop. The expected output is shown below.
Hello
0! is 1
1! is 1
2! is 2
3! is 6
4! is 24
5! is 120
6! is 720
7! is 5040
8! is 40320
9! is 362880
The full program with comments is shown next.
#include <stdio.h>
//This is a global
//it goes in the data section
int globalNumber=7;
//Factorial using a loop
int factorial(int x);
int main(int argc, char** argv){
//This variable is constant.
//It goes in the data section
const char* greeting = "Hello";
printf("%s\n",greeting);
//x is only scoped to this loop
//x is on the Stack
for(int x=0; x < 10; x++){
printf("%d! is %d\n",x,factorial(x));
}//x is deleted when the loop ends
//The below line will not work:
//printf("What is x? %d\n",x);
return 0;
}
//x is on the Stack
//it is a function parameter
int factorial(int x){
//total is on the stack it is
//a local
int total = 1;
//i is on the stack it is local
//to this loop
for(int i=1; i <= x; i++){
total = total * i;
}//i is released when this loop ends
return total;
}//total and x are released when this function
//ends
The actual instructions for this program are stored in the text part of memory. Things like the instructions for total = total * i. These never change, they just describe how the program works.
Globals and constants are stored in the data region. There is one global here int globalNumber=7;. There is also one constant const char* greeting = "Hello";. The memory needed by both these variables is prepared for by the compiler in the data region of the program.
We next have a function. The function is shown below without any comments for easy readability.
int factorial(int x){
int total = 1;
for(int i=1; i <= x; i++){
total = total * i;
}
return total;
}
The function has one parameter x. When the function is called the value of x will get space in the stack memory. The next local is total. This will also get space on the stack. When the loop starts, the variable i is created. This variable is local to the loop itself. It is still stored on the stack. Eventually, the loop will end and i will be released. It no longer exists as soon as the loop ends. The function then returns. When the function ends the memory for x and total are released. The return value is copied to whatever memory is assigned for it elsewhere.
All these scopes can lead to many very strange code. The following example reuses i in many distinct cases. This is a terrible design and you should not use it. It is just an example of how a single variable can have many different meanings in different parts of the code.
#include <stdio.h>
int i=7;//Global i
//Function parameter i
int badDesign(int i);
//Function that changes global
void updateI(int x);
int main(int argc, char** argv){
printf("main: Value of i at start: %d\n",i);
int i=0;//Local i
printf("main: Value of i after first statement : %d\n",i);
int temp = badDesign(9);
updateI(temp);
printf("main: Value of i before return statement : %d\n",i);
return 0;
}
int badDesign(int i){
int total=0;
printf("badDesign: Value of i before loop %d\n",i);
for(int i=0; i < 4; i++){
total = total + i;
printf("badDesign: Value of i in loop %d\n",i);
}
printf("badDesign: Value of i after loop %d\n",i);
return total*i;
}
void updateI(int x){
printf("updateI: Value of i at start %d\n",i);
i = x;
printf("updateI: Value of i at end %d\n",i);
}
The output of the code is shown below. Try to figure out why this happens.
badDesign: Value of i before loop 9
badDesign: Value of i in loop 0
badDesign: Value of i in loop 1
badDesign: Value of i in loop 2
badDesign: Value of i in loop 3
badDesign: Value of i after loop 9
updateI: Value of i at start 7
updateI: Value of i at end 54
main: Value of i before return statement : 0
Heap Memory Example¶
When we request memory on the heap, we just get the number of bytes we asked for. We get a pointer to the memory. We can do anything we want with it.
The below code asks to allocate space for 16 characters. We know a character is 1 byte, so we get 16 bytes.
int size=16;
char* ptr = malloc(size*sizeof(char));
We can fill this memory up with values. Remember that A is \(65\) is ASCII. Also, strings always end with a null.
for(int i=0; i < size-1; i++){
ptr[i]=65+i;
}
ptr[size-1]=0;
If we print this string we get the following output ABCDEFGHIJKLMNO. The value of ptr is just the memory address where this data lives. We can image the array looks like the following.
Position |
Letter |
ASCII Value |
|---|---|---|
ptr[0] |
A |
65 |
ptr[1 |
B |
66 |
ptr[2] |
C |
67 |
ptr[3] |
D |
68 |
ptr[4] |
E |
69 |
ptr[5] |
F |
70 |
ptr[6] |
G |
71 |
ptr[7] |
H |
72 |
ptr[8] |
I |
73 |
ptr[9] |
J |
74 |
ptr[10] |
K |
75 |
ptr[11] |
L |
76 |
ptr[12] |
M |
77 |
ptr[13] |
N |
78 |
ptr[14] |
O |
79 |
ptr[15] |
0 |
0 |
This is just binary data. I happen to be treating it as a string, but it is just memory. I can tell C to covert the pointer to a pointer to shorts. A short is a 2 byte number.
We can tell C to treat the memory as if it was an array of shorts instead.
short* ptrS = (short*)ptr;
//There are size/2 shorts in the array
for(int i=0; i < size/sizeof(short); i++){
printf("ptrS[%d]=%d\n",i,ptrS[i]);
}
This prints out the following.
ptrS[0]=16961
ptrS[1]=17475
ptrS[2]=17989
ptrS[3]=18503
ptrS[4]=19017
ptrS[5]=19531
ptrS[6]=20045
ptrS[7]=79
Where did these numbers come from. The data is just binary. Two characters have been combined into one short. The characters are treated as two parts of a larger number.
The first two characters are A and B. A is represented by 65 which is 0100 0001 in binary. B is represented by 66 which is 0100 0010. The value we read in the array is 16961. In binary this is 0100 0010 0100 0001. It is read from memory as BA. This gives us a hint to how C treats multi-byte number in memory. We know the data is stored as AB, but C treats that first byte as the higher order bits.
Position |
Value |
Reason |
|---|---|---|
ptrS[0] |
16961 |
\(66 * 256 + 65\) |
ptrS[1] |
17475 |
\(68 * 256 + 67\) |
ptrS[2] |
17989 |
\(70 * 256 + 69\) |
ptrS[3] |
18503 |
\(72 * 256 + 71\) |
ptrS[4] |
19017 |
\(74 * 256 + 73\) |
ptrS[5] |
19531 |
\(76 * 256 + 75\) |
ptrS[6] |
20045 |
\(78 * 256 + 77\) |
ptrS[7] |
79 |
\(0 * 256 + 79\) |
We can try converting the pointer to an integer pointer.
int* ptrI = (int*)ptr;
for(int i=0; i < size/sizeof(int); i++){
printf("ptrI[%d]=%d\n",i,ptrI[i]);
}
Integers are even bigger. Now, four characters are combined into a single number. The output of the code is shown below.
ptrI[0]=1145258561
ptrI[1]=1212630597
ptrI[2]=1280002633
ptrI[3]=5197389
We can again look back at the character values to see where the numbers came from.
Position |
Value |
Reason |
|---|---|---|
ptrI[0] |
1145258561 |
\(68*256^3 + 67*256^2 + 66*256 + 65\) |
ptrI[1] |
1212630597 |
\(72*256^3 + 71*256^2 + 70*256 + 69\) |
ptrI[2] |
1280002633 |
\(76*256^3 + 75*256^2 + 74*256 + 73\) |
ptrI[3] |
5197389 |
\(0*256^3 + 79*256^2 + 78*256 + 77\) |
The same memory is used, it is just being read in a different way. An even larger number is the long long. This is 8 bytes.
long long* ptrL = (long long*)ptr;
for(int i=0; i < size/sizeof(long long); i++){
printf("ptrL[%d]=%lld\n",i,ptrL[i]);
}
We only get three numbers this time.
ptrL[0]=5208208757389214273
ptrL[1]=22322617059592777
The calculations just get bigger and bigger.
Position |
Value |
Reason |
|---|---|---|
ptrL[0] |
5208208757389214273 |
\(\sum_{i=0}^{7} (65+i)*256^i\) |
ptrL[1] |
22322617059592777 |
\(0*256^7 + \sum_{i=0}^{6} (73+i)*256^i\) |
Since it is just memory, we can change one value with any pointer. For example, we can subtract from the pointer of shorts.
ptrS[0]=ptrS[0]-10;
If we print the string afterwards, we get 7BCDEFGHIJKLMNO. The binary data changed it is reflected in the first character.
Once we are done with the memory, we need to free it.
free(ptr);
The full source code for this example is given below.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char** argv){
int size=16;
//Request a pointer for size characters
char* ptr = malloc(size*sizeof(char));
//Put in 15 letters and a trailing null
for(int i=0; i < size-1; i++){
ptr[i]=65+i;
}
ptr[size-1]=0;
//Print the string to confirm it worked
printf("String: %s\n",ptr);
//A short is 2 bytes. We can pretend the
//pointer points to shorts
short* ptrS = (short*)ptr;
//There are size/2 shorts in the array
for(int i=0; i < size/sizeof(short); i++){
printf("ptrS[%d]=%d\n",i,ptrS[i]);
}
//An integer is 4 bytes
int* ptrI = (int*)ptr;
for(int i=0; i < size/sizeof(int); i++){
printf("ptrI[%d]=%d\n",i,ptrI[i]);
}
//A long long is 8 bytes
long long* ptrL = (long long*)ptr;
for(int i=0; i < size/sizeof(long long); i++){
printf("ptrL[%d]=%lld\n",i,ptrL[i]);
}
//Change a value in the short version
ptrS[0]=ptrS[0]-10;
//See how the string changed
printf("String After Change: %s\n",ptr);
//Release the memory when we are done
free(ptr);
//End function
return 0;
}
Resizing Array¶
When we read in strings earlier, we always had to set a maximum size to create our buffer. Here is our readFromStdin from before. It has a fixed buffer size of 100. That is the maximum it can read.
char* readFromStdin(){
//Create an array buffer
int bufferSize = 100;
char* buffer = malloc(sizeof(char)*bufferSize);
//Place characters into buffer starting at pos 0
int position = 0;
//Loop over characters
char temp;
temp = getchar();
while(temp != EOF && temp != '\n'){
buffer[position]=temp;
temp = getchar();
position++;
}
//Null Terminate the String
buffer[position]=0;
position++;
//Return the string we read in
return buffer;
}
With the heap, we do not need to have maximum sizes. We can resize the array as needed. If we run out of space, we just ask for more. To implement this, we will create our first Data Structure. A Data Structure is way to organize data in a computer. We saw in the previous section that we can use memory as different things. We can collect a series of bytes together and use them to mean whatever we want.
For our resizable array, we need to know three things.
A pointer to the array with the data.
The number of things currently in the array.
How far was can expand memory before we ask for more.
We are building this Data Structure with the expectation that it will expand. If we didn’t expect it to expand, we could just allocate an array of the correct size. With this assumption in place, it makes sense to allocate some extra memory. We cannot predict how much, so we make a guess. If we are wrong, we will need to allocate more memory.
We are planning to read in data of the char type to our resizing array. To make this work we more specifically need to know the following.
Eight bytes of space for a pointer to a
chararray.Four bytes of space for the current size.
Four bytes of space for the max size we can expand into.
In C, we can define a struct. This is a Data Structure. We explain to C how we want our data organized.
struct ResizeArray{
char* data;
int currentSize;
int maxSize;
};
This is telling C that we would like 16 bytes. We are going to use the first 8 bytes for a pointer to an array of characters. We are using the next 4 bytes for the current size of the array. We are using the last 4 bytes for the max size of the array. We can then access the parts of the memory we want as need. When we create a new struct it is often useful to give it a type name. Then we can just refer to it like we could int. We could refer to this structure as struct ResizeArray right now. If we want to just call it ResizeArray and not have to explicitly state it is a struct each time we need to add the following line.
typedef struct ResizeArray ResizeArray;
The format here is typedef [current name] [new alternative name]. You can create any types you want with this command, for example typedef int Cats;. This would create a new type called Cats that is just an single integer.
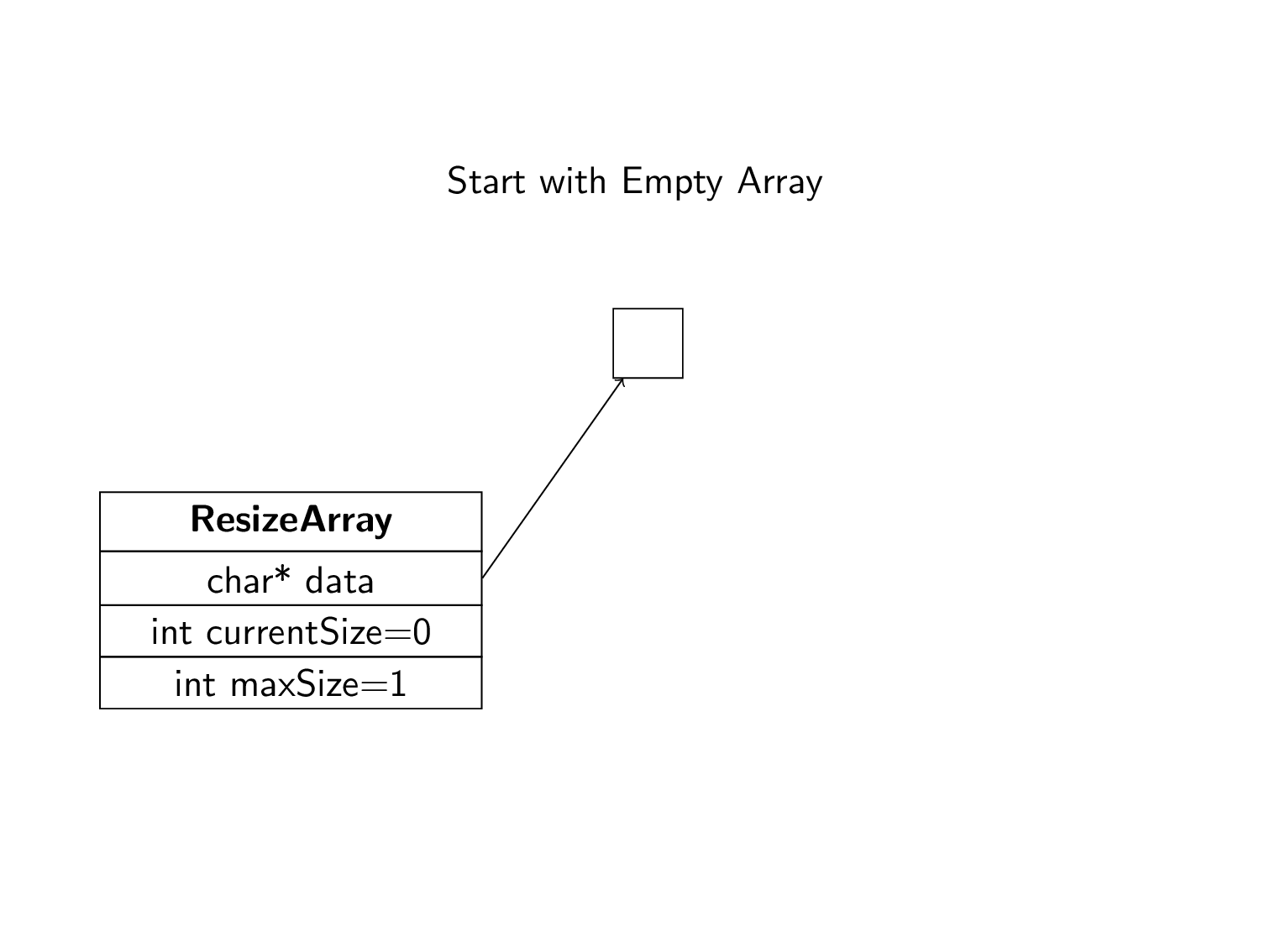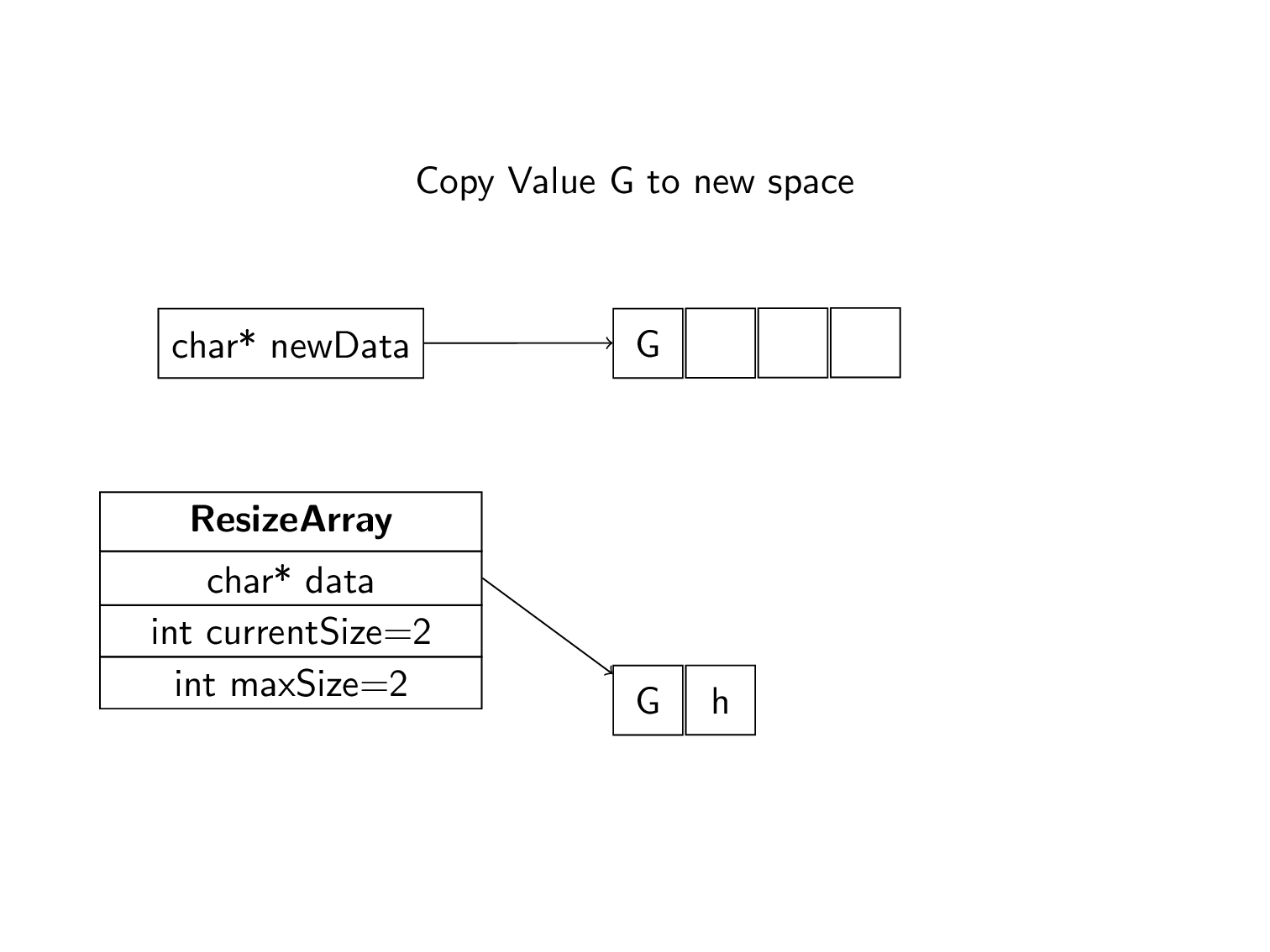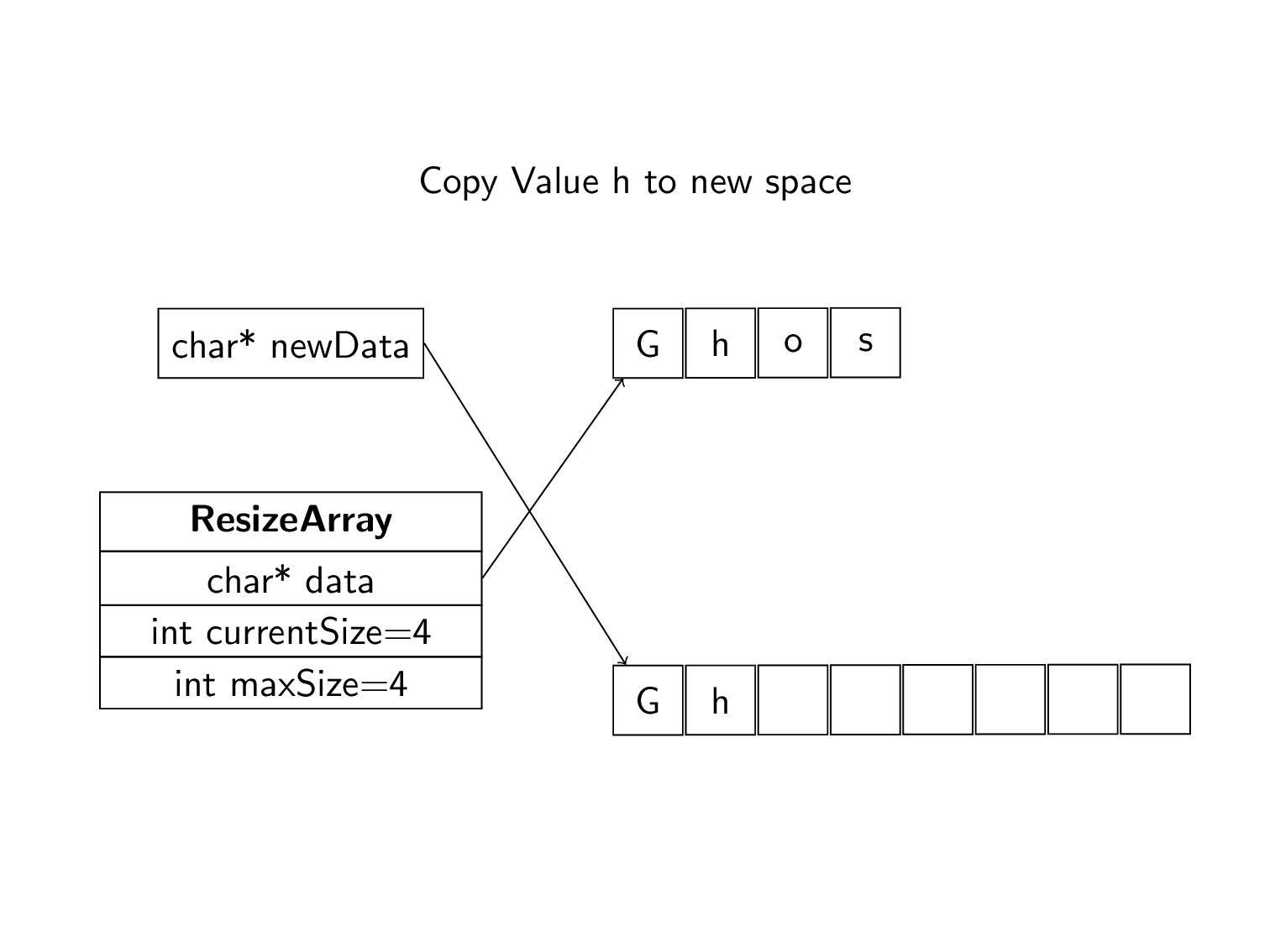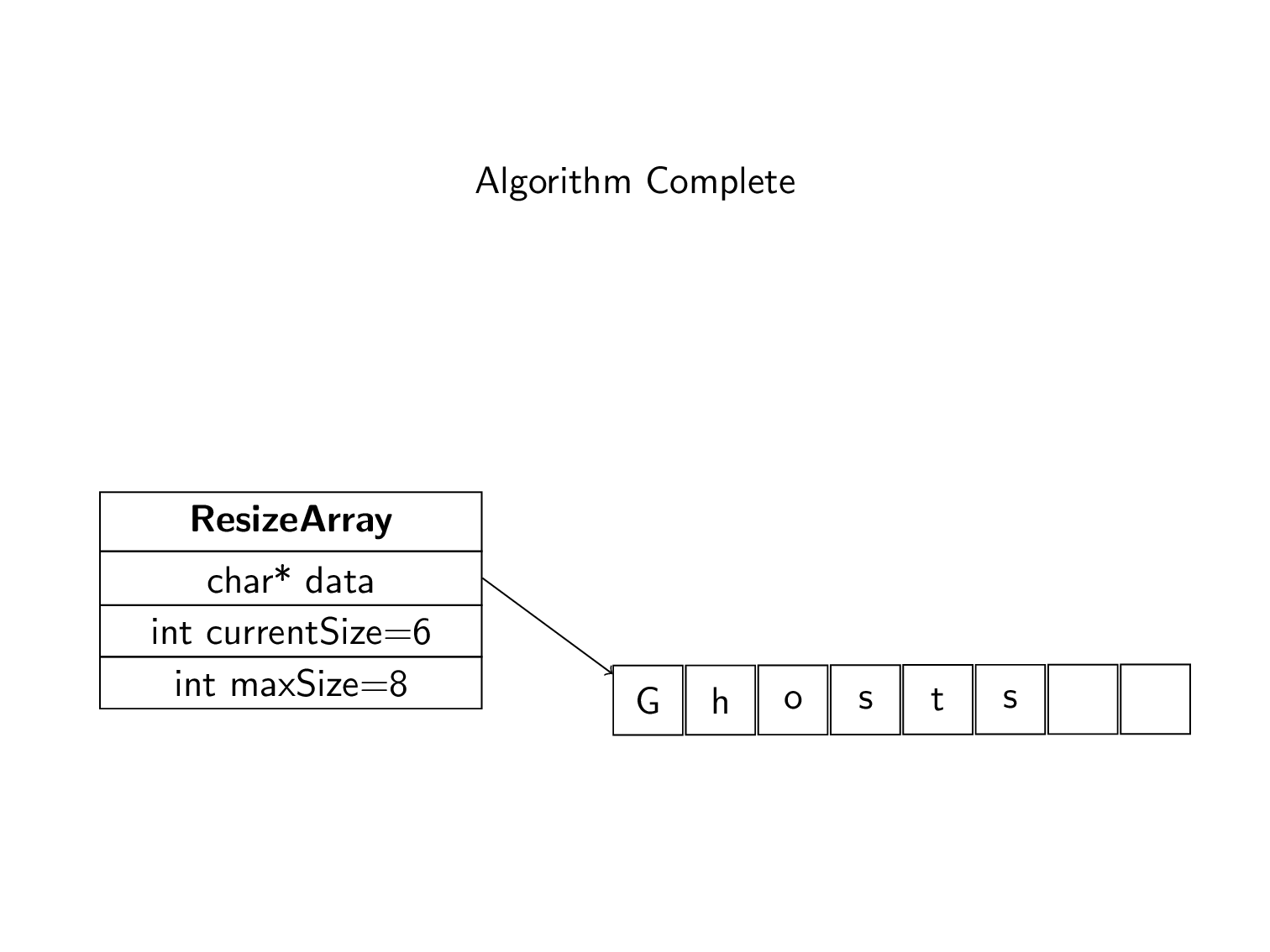
In the following animation, we read in the word “Ghosts”. Initially, the array starts with only one space. When it runs out of space, we copy the values to a new area of memory and move the pointer. The new area of memory has double the space of the old one. This process repeats until the whole word in inserted. Notice that at no point did we need to know how much space we needed to fit the word. The array grows as needed.
We will make functions to go with our Data Structure. This will make the structure easier to use. It also organizes our code better.
We need to be able to create a new ResizeArray. First, we need to allocate space for the Data Structure itself. We initialize the array with \(8\) spaces. The animation above started with only \(1\) space. As you saw, this immediately required a resize. Starting with \(8\) spaces gives us a little more space to work with. The array currently has nothing in it. We set the current size to be \(0\). We then use malloc to make our initial array. We return a pointer to the Data Structure.
ResizeArray* makeArray(){
//Get space for our data structure
ResizeArray* RA = malloc(sizeof(ResizeArray));
//Start with 8 spaces
RA->maxSize = 8;
//No values in the array yet
RA->currentSize = 0;
//Request space for the array
RA->data = malloc(RA->maxSize * sizeof(char));
return RA;
}
We may want to know the current size of the ResizeArray. We make a function to ask this.
int size(ResizeArray* RA){
return RA->currentSize;
}
We also might need direct access to the array at some point.
char* getArray(ResizeArray* RA){
return RA->data;
}
Our primary goal was to add elements to the array. The following function inserts a new element at the end of the array. If their is still empty space in memory, we just add the new element into the array and increase currentSize. If not, we need to increase the size. This is handled by another function called expand.
void append(ResizeArray* RA, char letter){
//Make sure we have space
if(RA->currentSize+1 > RA->maxSize){
expand(RA);
}
//Add the element to the end
RA->data[RA->currentSize]=letter;
//Update the Size
RA->currentSize++;
}
If we need to expand the array, we make a new array with double the size. we don’t want to just add one extra space, then we will be copying all the time. Doubling adds a significant amount of space, but it is also relative to the current amount of space. Initially, we make smaller increases. As the array gets bigger, the increases also get bigger. It is very important that we free the old array. It is no longer needed and we don’t want to fill up our memory with useless arrays we are no longer using.
void expand(ResizeArray* RA){
//Make an array of double size
char* newData = malloc((RA->maxSize*2) *sizeof(char));
//Copy the values into the new array
for(int i=0; i < RA->maxSize; i++){
newData[i] = RA->data[i];
}
//Free the old array
free(RA->data);
//Point to the new array
RA->data = newData;
//Update Data Structure so it knows about new space
RA->maxSize = RA->maxSize*2;
}
Using this Data Structure, we can write a new readFromStdin that doesn’t know or care how many characters it needs to read it. In will read in as many characters as it needs to.
char* readFromStdin(){
//Make a Resizing array
ResizeArray* buffer = makeArray();
//Read Characters
char temp = getchar();
while(temp != EOF && temp != '\n'){
append(buffer,temp);
temp = getchar();
}
append(buffer,'\0');
return getArray(buffer);
}
What is the runtime of this new algorithm? What is it’s memory usage? We can start with an example. Let’s imagine we want to read in the alphabet. It has 26 letters.
ABCDEFGHIJKLMNOPQRSTUVWXYZ
The following table shows how the algorithm runs.
|
|
Stored Letters |
Work Done |
Comments |
|---|---|---|---|---|
0 |
8 |
None |
\(O(1)\) |
Initialize Space |
1 |
8 |
A |
\(O(1)\) |
Insert A |
2 |
8 |
AB |
\(O(1)\) |
Insert B |
3 |
8 |
ABC |
\(O(1)\) |
Insert C |
4 |
8 |
ABCD |
\(O(1)\) |
Insert D |
5 |
8 |
ABCDE |
\(O(1)\) |
Insert E |
6 |
8 |
ABCDEF |
\(O(1)\) |
Insert F |
7 |
8 |
ABCDEFG |
\(O(1)\) |
Insert G |
8 |
8 |
ABCDEFGH |
\(O(1)\) |
Insert H |
8 |
16 |
ABCDEFGH |
\(O(n)\) with \({n=8}\) |
Copy 8 Elements |
9 |
16 |
ABCDEFGHI |
\(O(1)\) |
Insert I |
10 |
16 |
ABCDEFGHIJ |
\(O(1)\) |
Insert J |
11 |
16 |
ABCDEFGHIJK |
\(O(1)\) |
Insert K |
12 |
16 |
ABCDEFGHIJKL |
\(O(1)\) |
Insert L |
13 |
16 |
ABCDEFGHIJKLM |
\(O(1)\) |
Insert M |
14 |
16 |
ABCDEFGHIJKLMN |
\(O(1)\) |
Insert N |
15 |
16 |
ABCDEFGHIJKLMNO |
\(O(1)\) |
Insert O |
16 |
16 |
ABCDEFGHIJKLMNOP |
\(O(1)\) |
Insert P |
16 |
32 |
ABCDEFGHIJKLMNOP |
\(O(n)\) with \(n=16\) |
Copy 16 Elements |
17 |
32 |
ABCDEFGHIJKLMNOPQ |
\(O(1)\) |
Insert Q |
18 |
32 |
ABCDEFGHIJKLMNOPQR |
\(O(1)\) |
Insert R |
19 |
32 |
ABCDEFGHIJKLMNOPQRS |
\(O(1)\) |
Insert S |
20 |
32 |
ABCDEFGHIJKLMNOPQRST |
\(O(1)\) |
Insert T |
21 |
32 |
ABCDEFGHIJKLMNOPQRSTU |
\(O(1)\) |
Insert U |
22 |
32 |
ABCDEFGHIJKLMNOPQRSTUV |
\(O(1)\) |
Insert V |
23 |
32 |
ABCDEFGHIJKLMNOPQRSTUVW |
\(O(1)\) |
Insert W |
24 |
32 |
ABCDEFGHIJKLMNOPQRSTUVWX |
\(O(1)\) |
Insert X |
25 |
32 |
ABCDEFGHIJKLMNOPQRSTUVWXY |
\(O(1)\) |
Insert Y |
26 |
32 |
ABCDEFGHIJKLMNOPQRSTUVWXYZ |
\(O(1)\) |
Insert Z |
Notice that after we do a copy, we get a sequence of \(O(1)\) inserts because we have space available. If we total the above actions we get the following table.
Action |
Count |
|---|---|
Inserts |
26 |
Copies |
\(8+16=24\) |
In general, how many times will we need to copy a value. Let’s assume that we are working with large arrays, so starting at \(8\) vs \(1\) won’t really make much of a different. To make the math easier, we will work from \(1\) memory space up. The amount of space we will need to store \(n\) elements is \(2^k\) where \(2^{k-1} < n \le 2^k\). We want the closest power of two that is greater than or equal to \(n\).
We can figure out the closest power of two by computing \(\lceil \log_{2}(n) \rceil\). We round up the \(\log\) to the nearest whole number.
Look at what happens after a copy in the table. When we make copy 8 elements from to make more room, that is followed by 8 inserts that are \(O(1)\). Then when we make a copy of 16 elements, we have space to insert 16 times before we need to do it again. We can amortize these copies. Instead of imagining that the copy happens all at once, we can imagine the copy is paid for along with the later inserts. When we double the size and copy the array, we pay ahead for the next block on inserts. Imagine we started with a memory size of just 1 elements.
Memory Size |
Comments |
|---|---|
1 |
We can insert 1 element in constant time |
2 |
We copy 1 element to get to size 2 |
2 |
We can insert 1 element in constant time |
4 |
We copy 2 elements to get to size 4 |
4 |
We can insert 2 elements in constant time |
8 |
We copy 4 elements to get to size 8 |
8 |
We can insert 8 elements in constant time |
16 |
We copy 8 elements to get to size 16 |
16 |
We can insert 16 elements in constant time |
32 |
We copy 16 elements to get to size 32 |
32 |
We can insert 16 elements in constant time |
64 |
We copy 32 elements to get to size 64 |
64 |
We can insert 32 elements in constant time |
128 |
We copy 64 elements to get to size 128 |
128 |
We can insert 64 elements in constant time |
Each element that is inserted into the array pays two costs. It pays once to be inserts. It also pays retroactively for the copy that was needed to get its space.
When we are inserting elements, amount of memory needed will be \(O(2^{\lceil{ \log_{2}{n} \rceil}})\) which was can easily simplify to \(O(n)\). That is the amount of space in the final array. Along the way, we make copies. At certain points in the algorithm we may have two arrays in memory. We always free the space when we are done, so we will never be using more than double the number of characters \(n\) at any time. The memory usage will be \(O(2n)=O(n)\).
The runtime is also \(O(n)\). Each copies pays for a number of free inserts following it. It we look over the course of the entire insert, we will do about \(2n\) actions. That is also \(O(n)\). That means our algorithm is still linear time.
Realloc¶
C provides a function called realloc. This function attempts to resize the memory pointed to. The key thing to remember is that realloc does not always have enough space to increase the memory. For an array, the data must be continuous. If there is not enough space to expand the array, realloc will do the same thing we did. It will copy all the elements to a new section of heap memory with enough space to fit the new request. It implements the same conceptual algorithm we did above. If there is some extra space available it is used. If not, it needs to get more space and copy the data. Don’t assume that realloc will always succeed without having to do a copy.
One problem with this whole approach comes from the array itself. An array must be a set of continuous values. They all need to be next to each other in memory. This is not something we need to require. We can divide up things and place them in different areas of memory. We will see how to do this with our next Data Structure.
