.md .pdf

Contents

Search Analysis

Background

Locked-in syndrome is a very rare neurological disorder [Bruno and Laureys, December 2012]. A person with locked-in syndrome is cognitively intact. They can think clearly, but their body is shut down. They cannot move any part of their body. Many people with this syndrome have one or two minor motions they can perform such as blinking and eye.

If a person can move an eye, then they can at least communicate with the outside world. At best this means being able to respond to yes/no questions. With the ability to answer yes/no questions, science can build means of communication [Parker, 2003]. Research has even been done on building a web browser using direct brain-computer interfaces [Karim et al., 2006].

Journalist Jean-Dominique Bauby was one person who was stricken with locked in syndrome after a stroke [Bauby, 1998]. Working with partners, he wrote a book about his life. Every letter was dictated by answering yes/no questions about what the next letter should be. His book, The Diving Bell and the Butterfly was published in 1997 [Bauby, 1998].

In The Power Of Computational Thinking, the author look at Mr. Bauby’s dictation system as a computer science problem [Mcowan and Curzon, 2017]. This will provide the inspiration for this section. We can relate Big Oh to a an actual human task instead of computer operations.

Linear Search

How can we use the linear search algorithm to help a person with locked-in syndrome communicate?

First, we need to decide what array we are searching. We need all the letters of the alphabet. We also need a few special symbols. The person typing needs to be able to add periods, spaces, and stop typing. We will need to assign a special symbol for ending. We will use the exclamation point ! to mean end typing. We end up with the following symbol list.

//The alphabet used to select possible letters.
Let alphabet = " !.abcdefghijklmnopqrstuvwxyz"

We have a fixed size of 29 symbols. Our user cannot tell us what the target is, if that were true it would be easy. We need to ask questions. Eventually we will find the letter they want.

Counting blinks is most likely not something handled by most programming languages. This would need special hardware. At the most basic level, we are still getting a bool value as the answer. We can represent this by a function that asks yes/no questions. How this function works isn’t relevant to the search itself. It could be test, graphics, or blinking.

//Ask if the letter is the one the user is thinking. True means yes.
Function isLetter(letter)

We have a special case. What is the user never says yes? Maybe they want to end. Maybe they made a mistake. Humans make mistakes. We need to account for this. It make sense to loop back to the top and try again.

We can make this into an algorithm.

Function linearSearch(alphabet,count)
    While letter not selected do
        If (is correct letter) then
            Return letter
        End If
        Move to next letter
    End While
End Function

This would allow our user to communicate. How effective would it be? In the best case, the letter we need is one of the first few. In the worst case, the user needs to cycle through all 29 symbols to get to the last one. Every time the user needs to type a letter, they need to answer up to 29 yes/no questions. Each of these questions will be answered by blinking.

Let us assume that the letters average out and each one costs about \(29/2=15\) questions. To type out a sentence with 20 characters, we are asking the user to blink \(15*20=300\) times.

This is a functional solution, but it might not be the best one. Asking a computer to do things hundreds of times doesn’t seem like much. Asking a paralyzed patient to blink yes/no 300 times is a different story. We can do better.

Binary Search

How can we adapt the Binary Search for our user with locked-in syndrome? We need to adapt the algorithm into yes/no questions. Remember, that is the only way our user can communicate with us.

We still have the same list of potential letters.

//The alphabet used to select possible letters.
Let alphabet = " !.abcdefghijklmnopqrstuvwxyz"

We can also assume that our user is smart enough to understand where the special characters fall in the ordering.

We can start by asking “Is the letter between Space and and l?” We will need a new function to deal with this new question.

//Ask if the letter is between to (inclusive)
Function isLetterBetween(firstLetter, secondLetter)

We asked “Is the letter between Space and and l?” If the user says yes, we eliminate m-z. If the user no, we can eliminate Space-l. Either way, we cut the search space in half.

The adapted binary search algorithm is given below. Remember, we are taking to a human here. They can make mistakes. They might make a mistake and say yes/no unintentionally. This would lead to the restart conditions. We need to start again because they made a mistake.

Function binaryLetterSearch(letters, start, stop)
    //Case 1: No Letters to ask about. Restart
    //We didn't get an answer
    If start > stop then
        Restart
    End If
    //Case 2: Only one letter in range
    If start == stop then
        Ask if this is the correct letter
        If answer is yes then
            Return letter we found
        End If
        //Answer was no
        Restart
    End If
    //Case 3: There is a range to ask about
    Let middle = start + (stop-start)/2
    Let answer = isLetterBetween(letters[start], letters[middle])
    If answer is yes then
        //Search First Half
        Return binaryLetterSearch(letters, start, middle)
    End If
    //Search Second Half
    Return binaryLetterSearch(letters, middle+1, stop)
End Function

How many questions will we need to ask now? There are 29 possible letters. It is not always possible to divide evenly in half. For our estimation, we will take the worst case.

1. Ask about letter at position 14. We get left with either 15 or 14 possible options.

2. Assuming 15 letters were left, we ask again. We are left with either 7 or 8 letters.

3. Assuming 8 letters were left, we ask again. We are left with 4 letters.

4. We ask again. We are left with 2 letters.

5. We ask again. We are left with 1 letter.

6. We ask if it is the correct letter.

At most we need to ask 6 questions. Actually, it takes us 5 questions to determine the letter. We ask one other question to verify no mistakes were made. Since we are working with a human, they can make mistakes.

With the linear search, we estimated 300 questions to type out 20 characters. With this new algorithm, the user only needs to answer 6 questions per character. To type the same 20 characters, they need only 120 questions. A significant reduction in work on the users part.

Binary Search vs Linear Search

We can compare the two solutions formally using Big-Oh analysis.

Note

This analysis is also called Asymptotic Analysis. There are other types of Asymptotic Analysis. Big-Oh Analysis is more specific, it also tells you the specific method we are using.

Linear Search Analysis

The linear search looked through an array with \(n\) letters. What is the number of yes/no questions asked as an expression in \(T(n)\)?

In the worst case, we need to ask a question about every letter. That means we need to ask \(n\) questions. In the best case, we will ask just 1 question. On average, the letter we want could fall somewhere in the middle \(\frac{n}{2}\).

We know that \(\frac{n}{2} = O(n)\) because it is just hiding the constant \(\frac{1}{2}\). The worst case is trivially \(n=O(n)\). It is also true that \(1 \le n\), so we can also say that \(1=O(n)\) is a loose upper bound on the best case.

The worst case number of questions asked by our linear search is \(O(n)\). It is a linear time algorithm.

Binary Search Analysis

The binary search analysis is a little harder. We still have \(n\) letters and \(T(n)\) is the number of yes/no questions.

How does the code work? We ask one question, then we either find the answer or we divide \(n\) in half. We only need to search half the remaining elements.

We will describe this recursively. We need to ask one question, then search a list of \(\frac{n}{2}\) elements.

\( \begin{align} T(n) =& 1 + T(\frac{n}{2}) \\ T(1) =& 1 \end{align} \)

We need to find a pattern in this formula. Since the function uses division by 2, a good place to start is powers of 2 as inputs.

\( \begin{align} T(1) =& 1 \\ T(2) =& 1+T(1)=2 \\ T(4) =& 1+T(2)=3 \\ T(8) =& 1+T(4)=4 \\ T(16) =& 1+T(8)=5 \\ T(32) =& 1+T(16)=6 \end{align} \)

Note

Every non-power of two will fall between this values. We can just imagine they round up. We will be within a constant multiplier. We can estimate \(T(19)=6\). We will still be in the Big-Oh bound.

This might be enough to find the pattern, but we can find it more formally by expanding the expression.

\( \begin{align} T(n) =& 1+T(n/2) \\ =& 1+1+T(n/4) \\ =& 2+T(n/4) \\ =& 1+1+1+T(n/8) \\ =& 3+T(n/8) \\ =& 1+1+1+1+T(n/16) \\ =& 4+T(n/16) \\ =& 1+1+1+1+1+T(n/32) \\ =& 5+T(n/32) \end{align} \)

The pattern is more obvious here. At iteration \(k\) the formula is

\( \begin{align} T(n) =& k + T(n/2^k) \end{align} \)

How many times will this happen before it stops? When we get down to one character, we can stop asking questions.

The recursive pattern stops when we call \(T(1)\). To get to \(T(1)\), we need to do \(k\) iterations such that \(n/2^k=1\). The inside of the function is 1, so we know there is only 1 element left to search.

We need to solve this to find out how many iterations \(k\) are needed to get to \(T(1)\) in the recursive call.

\( \begin{align} \frac{n}{2^k} =& 1 \\ n =& 2^k \\ \log_2(n) =& k \end{align} \)

The function will end after \(k=\log_2(n)\) iterations. We can plug in this answer to the formula for \(k\) and simplify the recursion.

\( \begin{align} T(n) =& k + T(n/2^k) \\ =& \log_2(n) + T(n / 2^{\log_2(n)}) \\ =& \log_2(n) + T(n/n) \\ =& \log_2(n) + 1 \end{align} \)

The runtime of binary search is \(T(n) = 1+\log_2(n) = O(\log_2(n))\). The constant 1 doesn’t effect the Big-Oh class.

Comparison Results

We are comparing an \(O(\log_2(n))\) algorithm to an \(O(n)\) algorithm. The \(O(\log_2(n))\) grows slower and will therefore be a more efficient algorithm.

We can make a table with a few values to estimate how each function grows. We will use \(\frac{n}{2}\) for the linear search, assuming that on average it falls near the middle. This is actually an underestimate. We need to pick a constant \(c\) for to generate a table.

Size of Array	Linear Search Questions	Binary Search Questions
10	5	5
100	50	8
1,000	500	11
10,000	5,000	15
100,000	50,000	18
1,000,000	500,000	21
10,000,000	5,000,000	25
100,000,000	50,000,000	28
1,000,000,000	500,000,000	31

We can also plot the functions. Constant multipliers are required to draw a plot. We estimate linear search as \(\frac{n}{2}\). This give a reasonable average for the plot.

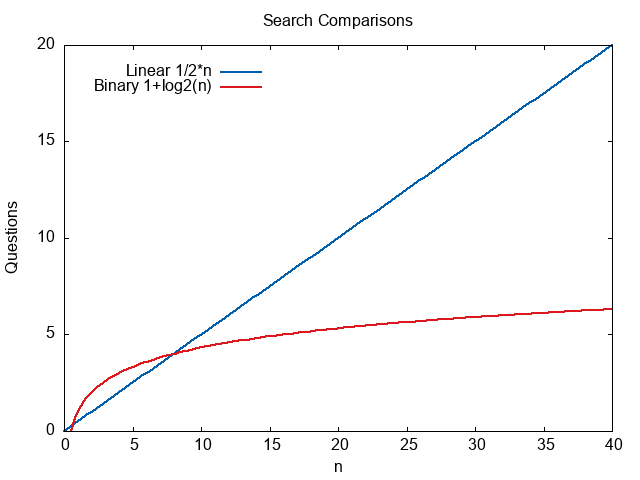
It should be clear from this table that the binary search approach asks significantly fewer questions.

previous

Algorithm Analysis

next

Sorting Data